8.3.1 事项时间参数
事项时间参数有三个:事项最早开始时间tE(j);事项最迟结束时间tL(i);事项时差Δt(i)。
1.事项最早开始时间tE(j)
事项最早开始时间是指从开始点事项到该事项最长路的时间总和。因此,作为一项任务首项工作的始点事项的最早开始时间等于零。某一箭头所指事项的最早开始时间,由它的箭尾事项的最早开始时间,加上本身工时决定。如果有多条箭线与箭头事项相连,即多条箭线射入某一事项的情况下,应选其中箭尾事项最早开始时间与相应工时相加之和的最大值为该事项的最早开始时间。用公式表示为
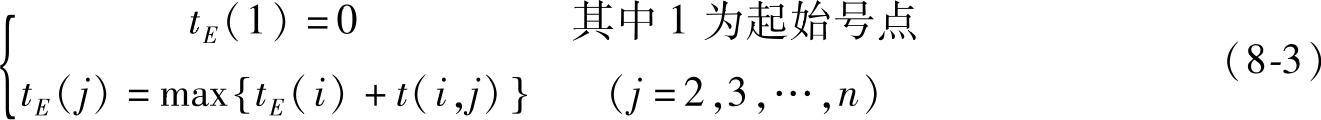
事项最早开始时间tE(j)的计算,应从始点开始,从左到右,顺箭头方向进行,结果用□括起,并标在相应的事项点旁。
[案例] 现有一个网络图(图8-10),计算各事项最早开始时间。
解:各事项最早开始时间tE(j)计算过程。
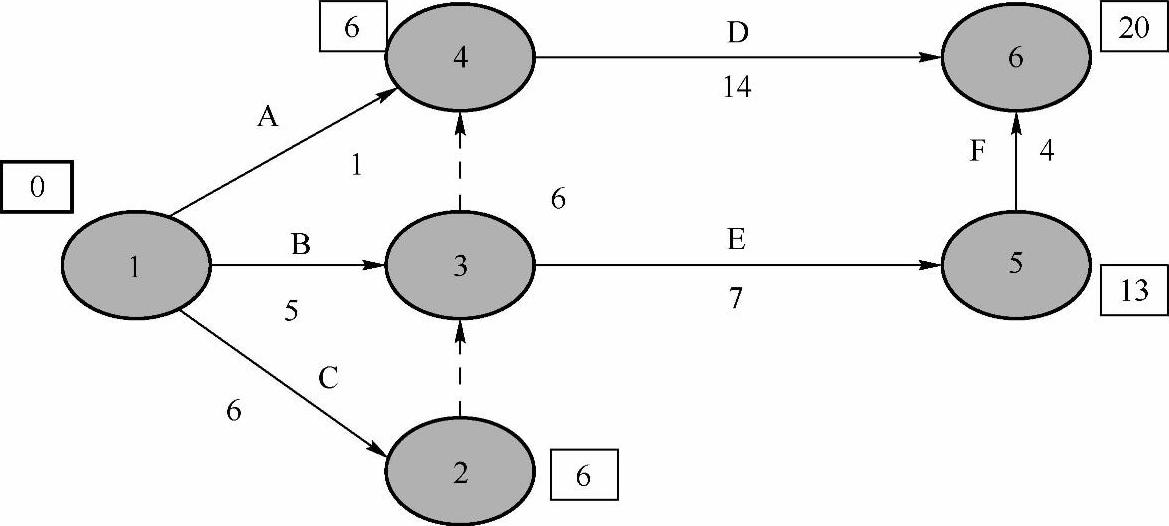
图8-10 网络图(带事项最早开始时间)
tE(1)=0
tE(2)=tE(1)+t(1,2)=0+6=6
tE(3)=max{tE(1)+t(1,3),tE(2)+t(2,3)}=max{0+5,6+0}=6
tE(4)=max{tE(1)+t(1,4),tE(3)+t(3,4)}=max{0+1,6+0}=6
tE(5)=tE(3)+t(3,7)=6+7=13
tE(6)=max{tE(4)+t(4,6),tE(5)+t(5,6)}=max{6+14,13+4}=20
把计算结果标注在原网络图8-10上。
2.事项最迟结束时间tL(i)
事项最迟结束时间是指如在这个时刻该事项不完工,就要影响其紧后各工作的按时开工和总工期,并巨数值与终点的最早开始时间相等,即从开始点到该事项最长路的时间总和。因此,作为一项任务首项工作的始点事项的最早开始时间等于零。一个箭尾事项的最迟结束时间,由它的箭头事项的最迟结束时间减去相应的工作时间决定。如果从此箭尾引出多条箭线,即存在多条箭线从该事项射出的情况下,应选其中箭头事项最迟结束时间与相应工时相加之差的最小值为该事项的最迟结束时间。以上分析过程用公式表示为
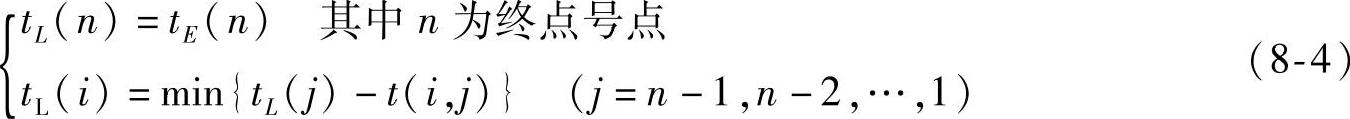
事项最迟结束时间tL(i)的计算,应从终点开始,从右到左,逆箭头方向进行,结果用△括起,并与表示事项最早开始时间tE(j)的□上下排列,标在相应的事项点旁。(https://www.daowen.com)
3.事项时差Δt(i)
事项时差是指在不影响整个项目完工期或下一个事项最早开始的情况下,该事项可以推迟的时间。用数学公式表示为
Δt(i)=tL(i)-tE(i) (8-5)
若时差为零,并满足条件
tE(j)-tE(i)=tL(j)-tL(i)=t(i,j) (8-6)的事项,成为关键事项。
[案例] 现有一如图8-11所示的网络图。计算各事项最迟结束时间。
解:事项最迟结束时间tL(i)计算如下
tL(6)=tE(6)=20
tL(5)=tL(6)-t(5,6)=20-4=16
tL(4)=tL(6)-t(4,6)=20-14=6
tL(3)=min{tL(5)-t(3,5),tL(4)-t(3,4)}=min{16-7,6-0}=6
tL(2)=tL(3)-t(2,3)=6-0=6
tL(1)=min{tL(4)-t(1,4),tL(3)-t(1,3),tL(2)-t(1,2)}=max{6+14,13+4}
=min{6-1,6-5,6-6}=0
把计算结果标注在原网络图8-11上。
很显然,在图8-11上,事项①、②、③、④和⑥为关键事项。所以线路C→D为关键线路。
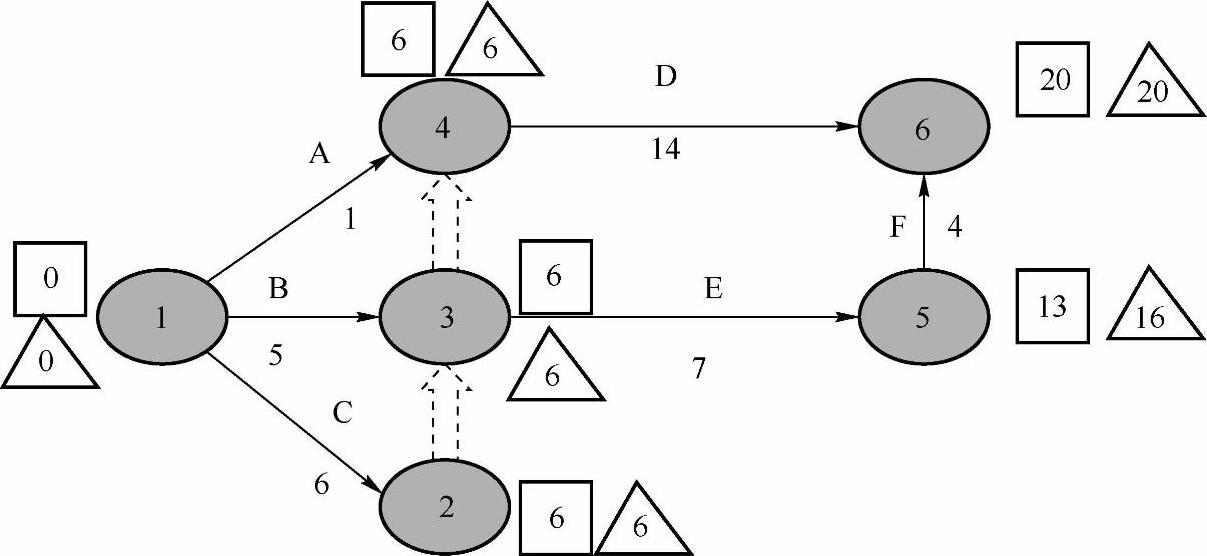
图8-11 网络图(带事项最迟给束时间)
