4.3 系统定量分析模型——状态空间建模法
有输入—输出法和状态变量法这两种既有联系又有区别的建模技术，来建立相应的定量分析模型即数学方程，并分析系统的动态特性。其中输入—输出建模法又称端部法，它只研究系统的传递关系，而不直接研究系统的内部结构。状态变量建模方法仍然是处理系统输入—输出关系的。但是在这些关系中，还附加了另一组变量，称为状态变量。在物理系统中，典型的变量有：振动位移（与弹性势能和重力势能有关）、振动速度（与动能和耗能函数有关）、振动加速度（与惯性力和惯性力矩有关）、电容上的电压（与它们存储的电场能量有关）、电感上的电流（与它们存储的电磁场能量有关）、温度（与热能有关）。状态变量建模方法可用于线性的或非线性的、时变的或时不变的，以及多输入多输出的系统，并巨更适用于计算机仿真，故应用相当广泛。
下面介绍与状态空间建模法有关的一些概念。
（1）系统状态 即指描述系统的运动状态（可以是物理的或非物理的）。
（2）状态变量 指能够完全描述动态系统时域行为的所含变量个数最少的变量组称为系统的状态变量。所谓完全描述系统的时域行为，指的是如果给定初始时刻t0的状态x（t0）和[t0，t]上的输入函数u（t），则系统在[t0，t]上任何瞬时的行为都由状态方程确定。
（3）状态向量 把x1（t），x2（t），…，xn（t）这几个状态变量看成是向量X（t）的分量，则X（t）称为状态向量。记作
或
XT（t）=[x1（t），x2（t）…，xn（t）] （4-2）
（4）状态空间 以状态变量x1（t），x2（t），…，xn（t）为坐标轴所构成的n维空间。在某一特定时刻t，状态向量X（t）是状态空间上的一个点。
（5）状态轨迹 以X（t）=X（t0）为起点，随着时间向前推移，X（t）在状态空间绘制出一条轨迹。
（6）状态方程——数学模型 由系统的状态变量构成的一阶微分方程组，称为状态方程。反映系统中状态变量和输入变量的因果关系，也反映每个状态变量对时间的变化关系。方程形式如下
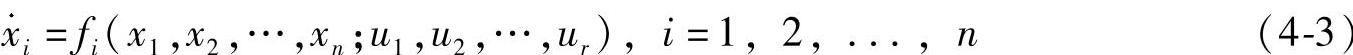
式中，n是状态变量个数；r是输入变量个数；fi是线性或非线性函数。
状态方程通用公式为
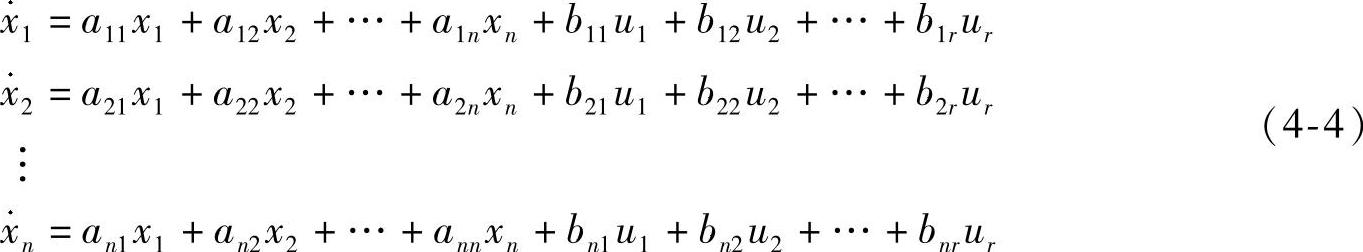
将通用公式化为以下矩阵形式
其中
x=[x1x2…xn]T，n维列向量。
u=[u1u2…ur]T，r维输入列向量。
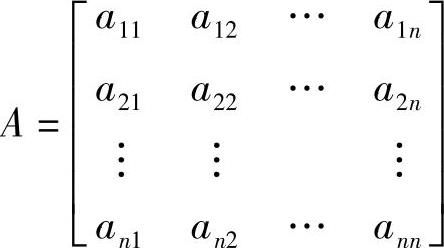，n×n维系统矩阵，表征各状态变量间的关系。
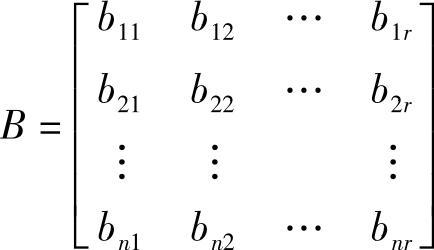，n×r维输入矩阵，表征输入对每个变量的作用。
（7）输出方程 输出方程指在给定输出的情况下，输出与状态变量和输入之间的函数关系。它反映了系统中输出变量与状态变量和输入变量的因果关系。方程形式如下
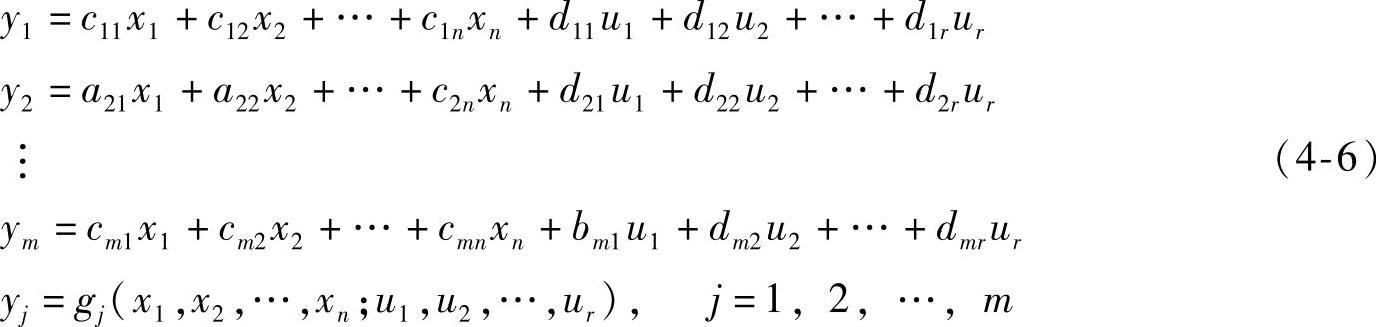
式中，n是状态变量个数；r是输入变量个数；m是输出变量个数；gj是线性或非线性函数。
通用公式为
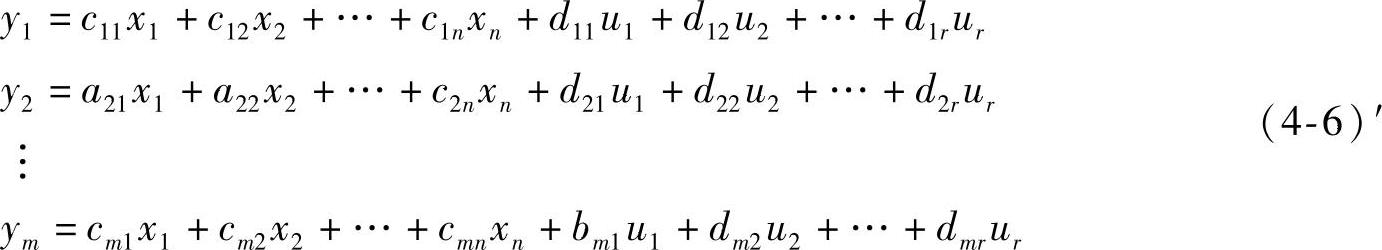
将通用公式化为如下矩阵形式
y=Cm×nx+Dm×ru （4-7）
其中
y=[y1y2…ym]T，m×1维输出向量。
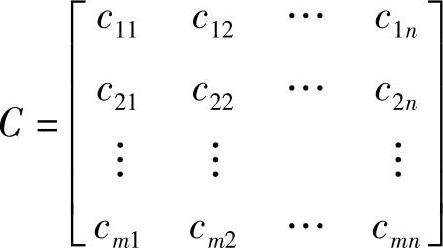，m×n维输出矩阵，它表征输出和每个状态变量的关系。
，
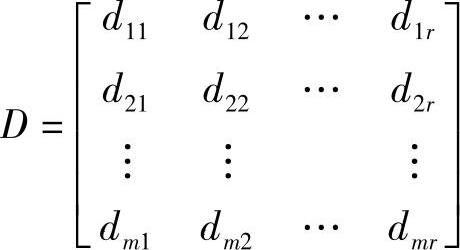D为m×r维前馈矩阵，它又称为直接转移矩阵。它表征了输入对输出的直接传递关系。
（8）动态方程或状态空间表达式 将状态方程和输出方程联立，就构成动态方程或状态空间表达式。一般形式如下
其中：A、B、C、D矩阵含义同上。
[举例]求如图4-2所示的RLC回路的状态空间表达式，也即建立以电压u1、u2为输入量，uA为输出量的状态空间表达式。
解：
1）选择状态变量：分别选择通过两个储能元件电感L1和电感L2的电流i1和i2为状态变量。
2）根据克希荷夫电压定律，列写2个回路的微分方程
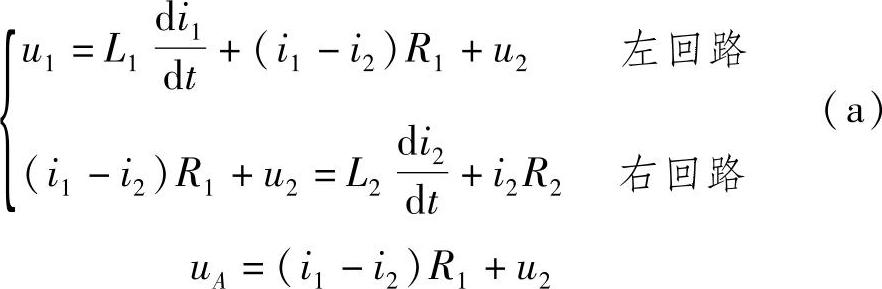
式中，u1、u2分别是电路中两个电源的电压。
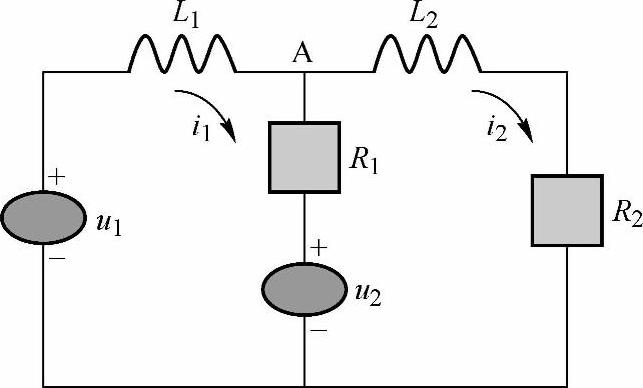
图4-2 RLC回路
3）状态空间表达式为
