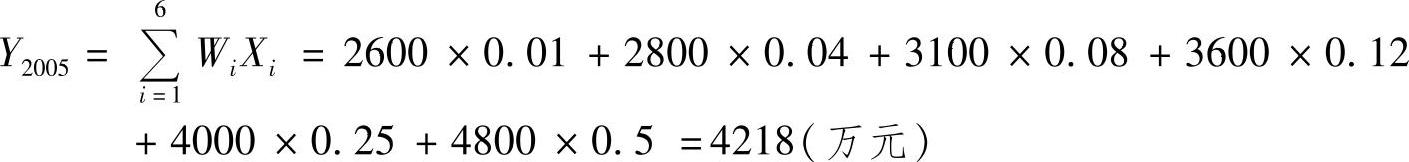6.3.1  平均预测法

6.3.1 平均预测法

1.简单算术平均法

简单算术平均法是时间序列预测法中一种最简单的方法，它是将观察期内预测目标时间序列值加总平均，求得算术平均数，并将其作为下期预测值。

预测计算公式为

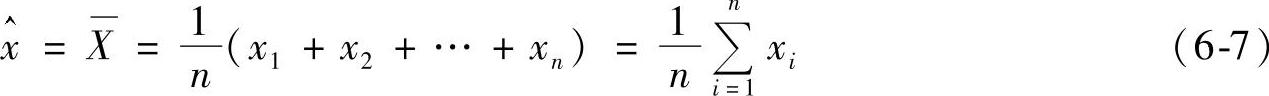
预测误差为

标准差

当样本为正态分布时，预测值发生在X士1S_X范围内的可能性为68%；发生在X士2S_X范围内的可能性为95.4%；发生在X士3S_X范围内的可能性为99.7%。

当样本数较大时，可用分组法计算预测值。具体的计算公式如下

均值：

标准差：

式中，m_i是第i组中值；f_i是第i组样本个数。

2.加权平均预测法

加权平均预测法是在简单平均法的基础上，对不同历史数据予以不同的加权系数，从而提高预测精度。

预测公式为

式中，Y是预测值；X_i是历史数据（i=1，2，…，n）；W_i是各历史数据对应的加权系数（i=1，2，…，n）。

平均预测法具有方法简单之优点，但预测结果不太精准，只适用于短期预测。

[案例] 某储蓄所历年的储蓄余额见表6-6。一般来说，越靠近现在，其权重越大，试预测2005年该储蓄所的储蓄余额为多少。

表6-6某储蓄所1999年至2004年期间的储蓄余额

解：