任务2 绘制锉配件的三视图
![]()
如图2-10所示,绘制锉配件的三视图,并分析其投影规律。

如图2-10所示,空间三个投影面两两垂直,将锉配件向三个投影面投射,分别得到三个方向的投影。想一想,三个投影有什么内在联系?如何将空间的三个投影表达在一个平面上?
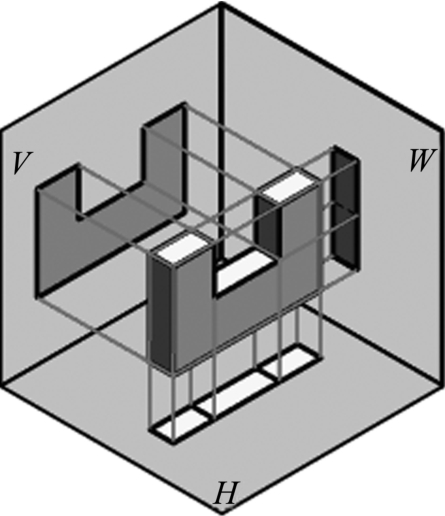
图2-10 锉配件的三视图

制作三面投影体系
![]()
在机械制图中,通常假设人的视线为一组平行的且垂直于投影面的投影线,这样在投影面上得到的正投影图,称为视图。
一个视图只能表达物体一个方向的形状,但不能表达物体的全部形状,要想表达物体的完整形状,就必须从物体的几个方向进行投射,绘制出几个视图,互相补充,才能将物体表达清楚。
通常我们在物体的后面、下面和右面放置三个投影面,从物体的前面、上面和左面进行投射,分别绘出三个视图,如图2-10所示。
一、三投影面体系的建立
三投影面体系由三个互相垂直的投影面所组成,如图2-11所示。三个投影面分别为:
正立投影面,正对着我们的投影面,简称为正面,用V表示;
水平投影面,水平放置的投影面,简称为水平面,用H表示;
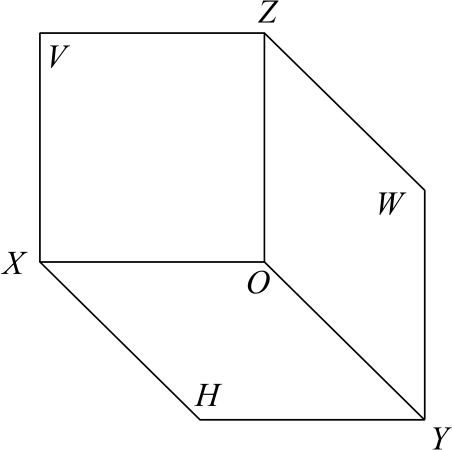
图2-11 三投影面体系
侧立投影面,右边侧立的投影面,简称为侧面,用W表示。
三个投影面的相互交线,称为投影轴。它们分别是:
OX轴:是V面和H面的交线,它代表长度方向,是X坐标;
OY轴:是H面和W面的交线,它代表宽度方向,是Y坐标;
OZ轴:是V面和W面的交线,它代表高度方向,是Z坐标;
三个投影轴垂直相交的交点O,称为原点,且沿坐标轴方向,离原点越远,坐标值越大。
二、三视图的形成
1.三视图的形成过程
将物体放在三投影面体系中,物体的位置处在人与投影面之间,用正投影法分别向三个投影面投射,得到三个视图,如图2-10所示。三个视图分别为:
(1)主视图:从前向后进行投影,在正立投影面(V面)上所得到的视图。
(2)俯视图:从上向下进行投影,在水平投影面(H面)上所得到的视图。
(3)左视图:从左向右进行投影,在侧立投影面(W面)上所得到的视图。
2.三投影面体系的展开
在实际作图中,为了画图方便,需要将三个投影面在一个平面(纸面)上表示出来。规定:使V面不动,H面绕OX轴向下旋转90°与V面重合,W面绕OZ轴向右旋转90°与V面重合,这样就得到了在同一平面上的三视图,如图2-12所示。在这里应特别注意的是:同一条OY轴旋转后出现了两个位置,因为OY是H面和W面的交线,也就是两投影面的共有线,所以OY轴随着H面旋转到OYH的位置,同时又随着W面旋转到OYW的位置。为了作图简便,投影图中不必画出投影面的边框,必要时投影轴也可以进一步省略。(https://www.daowen.com)
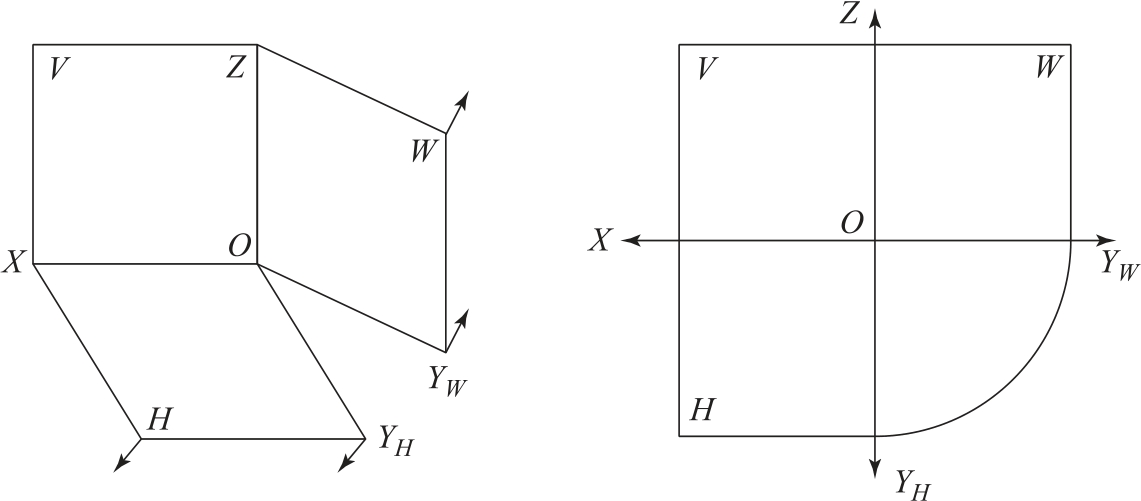
图2-12 三投影面体系的展开
三、三视图的对应关系
1.投影对应关系
从三视图的形成过程可以看出,三视图的位置关系是俯视图在主视图的正下方,左视图在主视图的正右方,按此位置配置的三视图,不需要注写其名称。
一个视图只能反映两个方向的尺寸,主视图反映了物体的长度和高度;俯视图反映了物体的长度和宽度;左视图反映了物体的高度和宽度,如图2-13(a)所示。
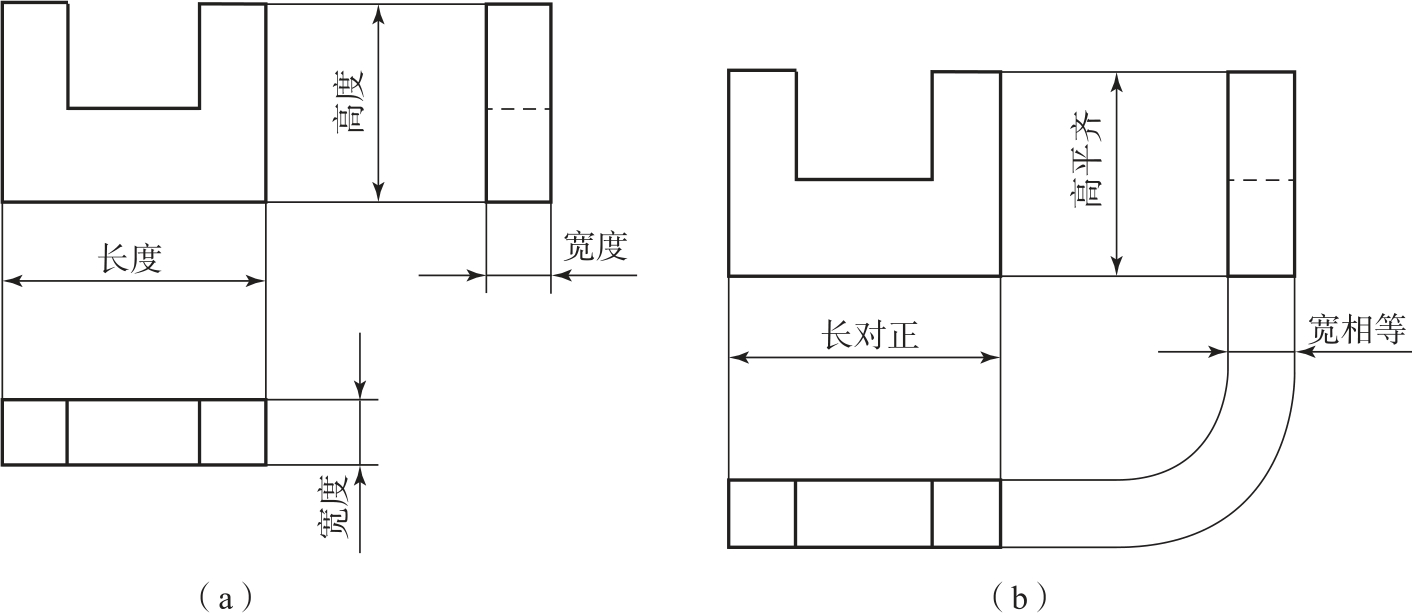
图2-13 视图间的“三等”关系

三面投影规律
由于物体在三投影面体系中投影时,相对三个投影面的空间位置是固定不动的,所以其三视图的长、宽、高有相互的对应关系,由此可以归纳出三视图的投影规律,如图2-13(b)所示,即:
主、俯视图“长对正”;
主、左视图“高平齐”;
俯、左视图“宽相等”。
三视图的投影规律反映了三视图的重要特性,也是画图和读图的重要依据。无论是整个物体还是物体的局部,其三面投影都必须符合这一规律。
2.方位对应关系
空间物体有前、后、左、右、上、下六个方位,根据三视图的展开过程,可以看出,物体六个方位在三视图中的对应位置,如图2-14所示。
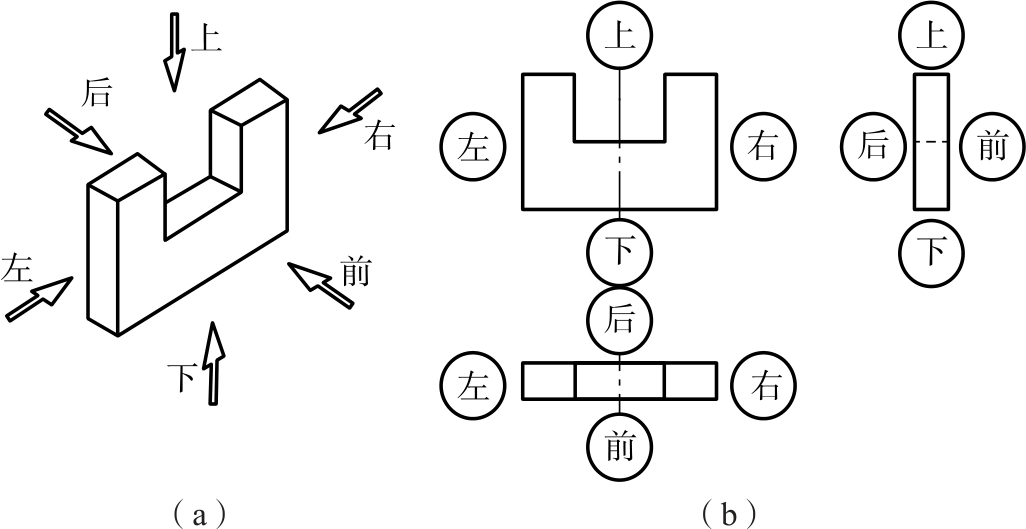
图2-14 立体图与三视图的方位对照
(a)立体图;(b)三视图
主视图反映了物体的上、下和左、右的相对位置关系;
俯视图反映了物体的前、后和左、右的相对位置关系;
左视图反映了物体的前、后和上、下的相对位置关系。
任务实施
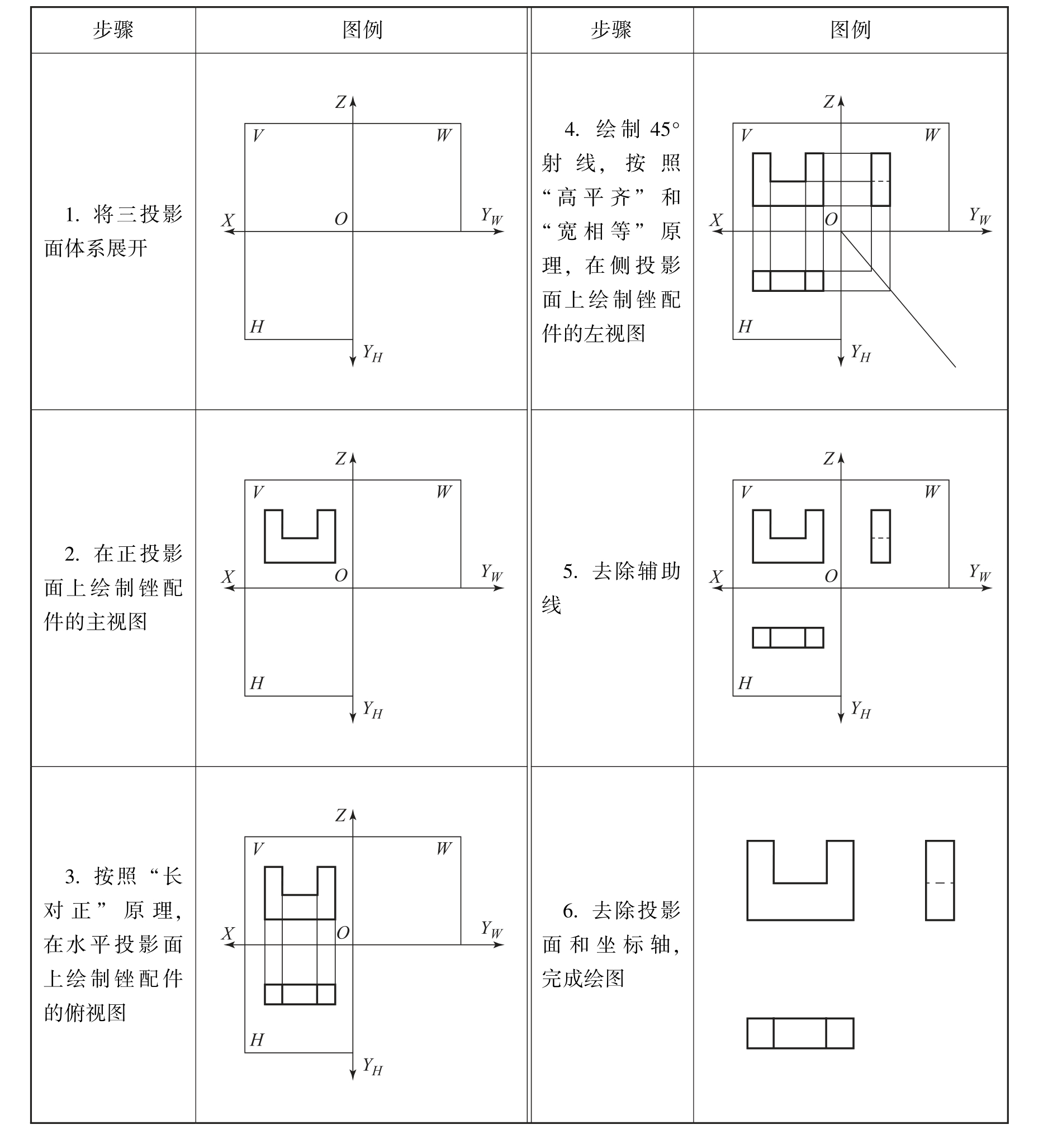
下面绘制图2-10所示锉配件的三视图。其绘图方法和步骤见表2-2。

绘制锉配件三视图
表2-2 锉配件三视图的绘图方法和步骤
![]()
根据图2-15所示补画左视图,并在三视图上标注物体的六个方位。
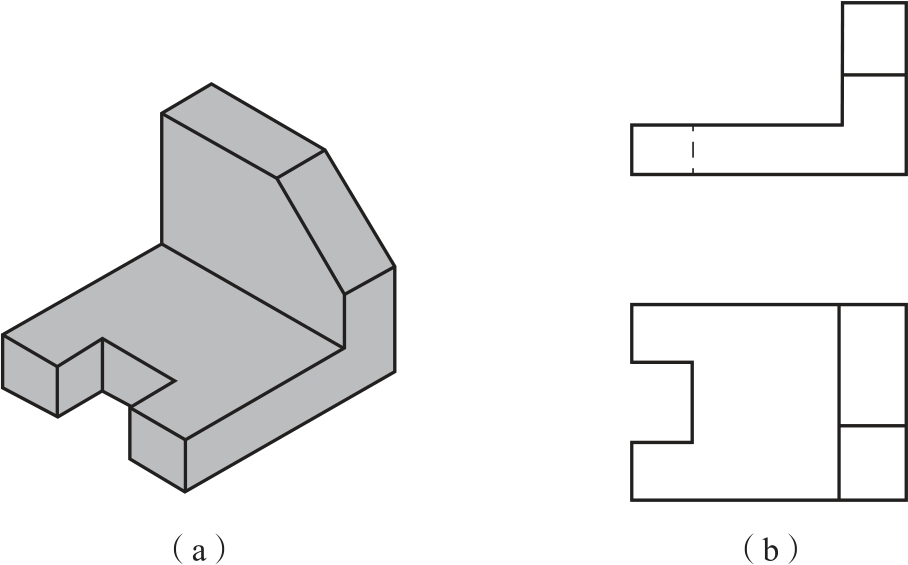
图2-15 压块
(a)立体图;(b)主、俯视图
