任务2 绘制圆柱的截交线
![]()
如图2-68(a)所示,一圆柱体被正垂面切割,该切割圆柱体的主、俯视图如图2-68(b)所示,试绘制其左视图。
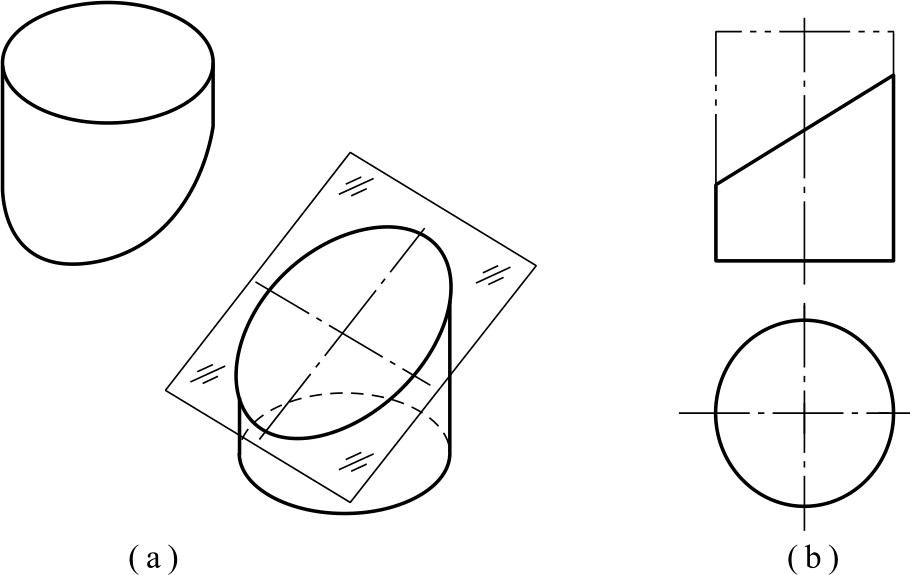
图2-68 正垂面切割圆柱的截交线
(a)立体图;(b)两视图

如图2-68所示,该圆柱被一个正垂面切割,所以其截交线的正面投影积聚为直线,又因为截交线上所有的点都是属于圆柱的侧面,所以它的水平投影积聚为圆形,试判断截交线侧面投影是什么形状?并思考该如何绘制。
![]()
截平面与曲面立体相交,其截交线种类比较多,有时是平面多边形,有时是封闭的平面曲线,其形状不仅和曲面立体的形状有关系,同时和截平面的位置也有关系。
曲面立体的形状主要有圆柱、圆锥、圆球、圆环之分,截平面位置又有垂直于轴线、平行于轴线、倾斜于轴线等几种不同情况,下面一一进行分析。
一、圆柱截交线
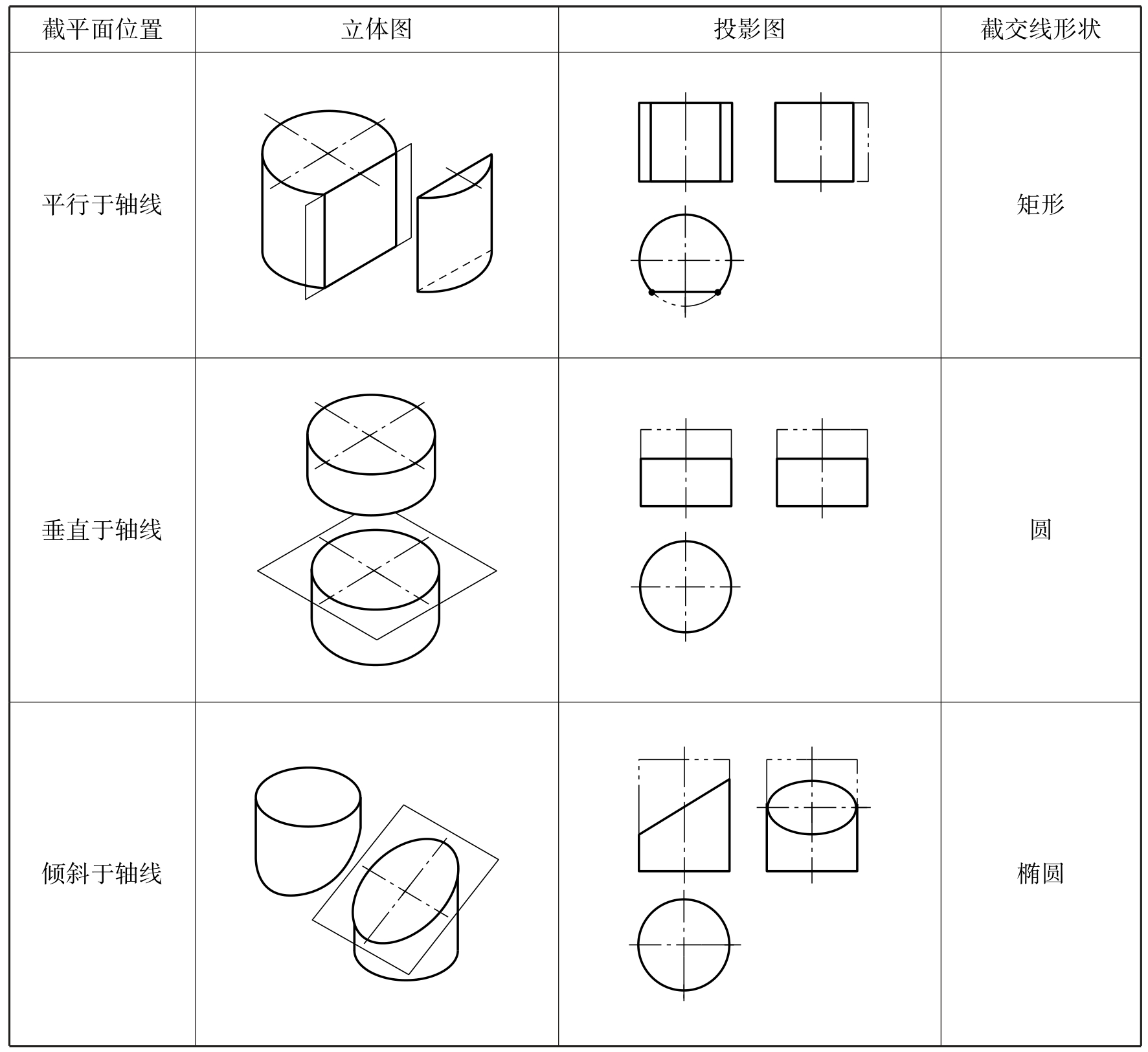
根据截平面与圆柱轴线的相对位置不同,圆柱截交线有三种情况,见表2-22。
表2-22 平面截割圆柱
二、斜割圆柱截交线的投影特性及画法
观察图2-68不难看出,平面斜割圆柱体时,平面与圆柱体的截交线为椭圆,由于该椭圆截交线是圆柱面和截割平面的共有线,因此它具有两个性质:
一是该椭圆所有的点都在圆柱侧面上,具有圆柱侧面的投影特性——水平投影积聚为圆;
二是该椭圆所有的点都在正垂截割平面上,具有正垂面的投影特性——正面投影积聚成直线。
因此该椭圆形截交线的正面投影和水平投影都是已知的。已知截交线的两面投影求第三面投影,可用求点的第三面投影的方法。
求截交线的第三面投影时,应先寻找特殊位置点,在该椭圆上有四个特殊位置点(又称为极限点),即最低点A、最高点B、最前点C、最后点D;其次再确定几个一般位置点,并求出一般位置点的第三面投影,依次连接各个点的第三面投影,即可得椭圆形截交线。
任务实施
绘制斜割圆柱左视图的具体作图步骤见表2-23。(https://www.daowen.com)

斜切圆柱
表2-23 绘制斜割圆柱的左视图具体作图步骤
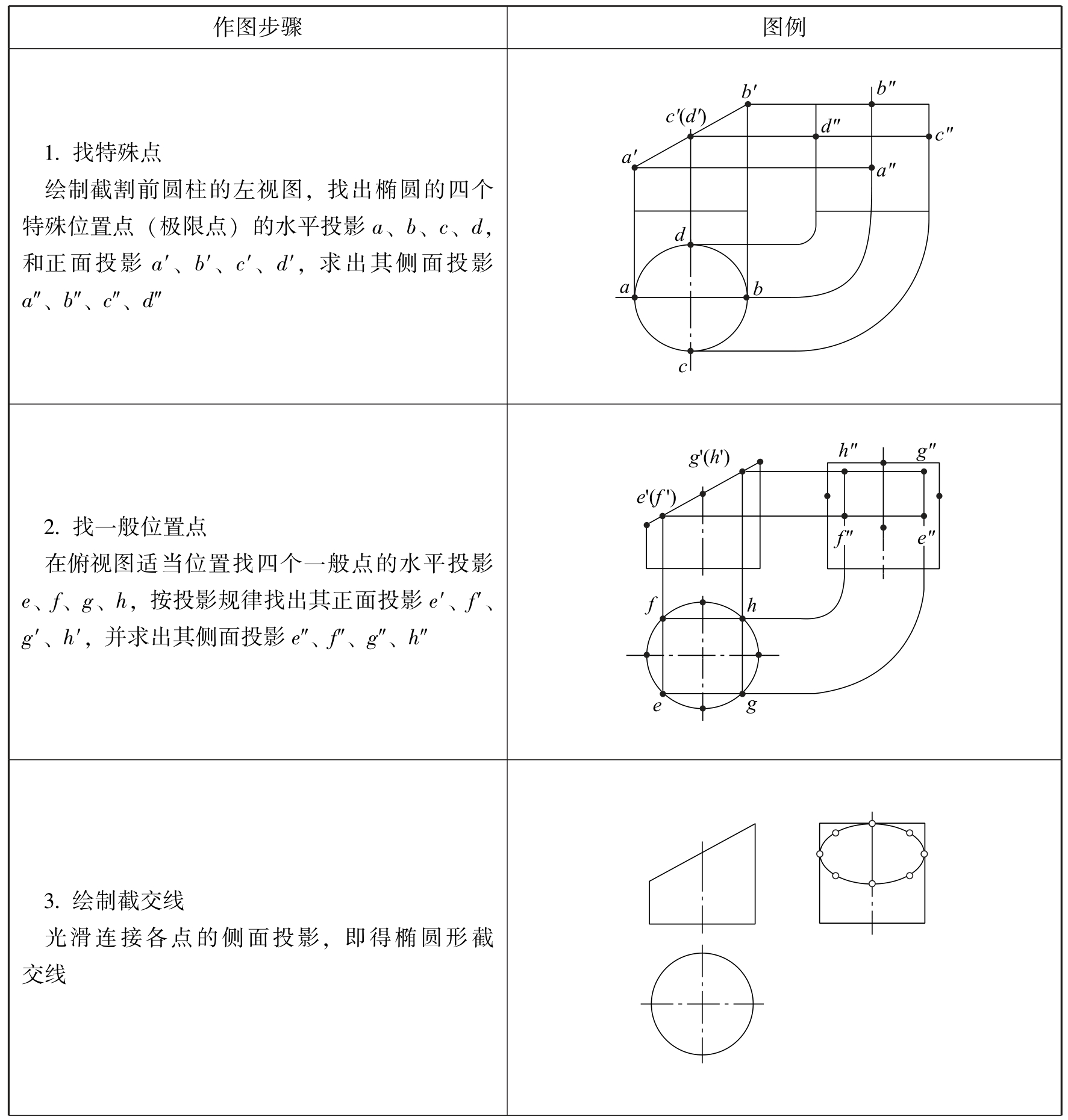
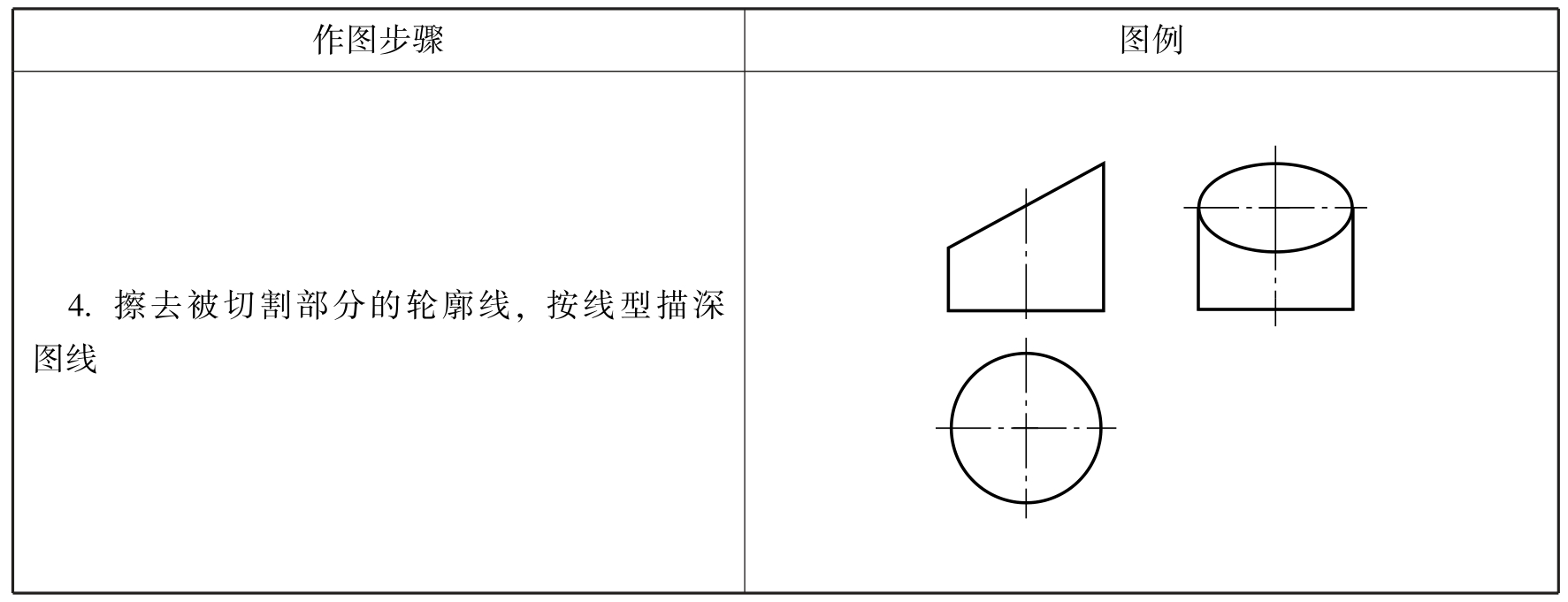
续表
![]()
圆柱的截交线
如表2-23所示,截平面倾斜于圆柱轴线时,截交线是椭圆,侧面投影也是椭圆。倾斜的角度不同,椭圆的大小不同,但当倾斜角度为45°时,截交线的侧面投影不是椭圆而是圆。
知识拓展
圆柱开槽的三视图
如图2-69所示圆柱的开槽,是由三个截平面共同切割形成的,所以绘制时,可分别分析三个截平面的投影特点,最后相交汇总成最终形状。
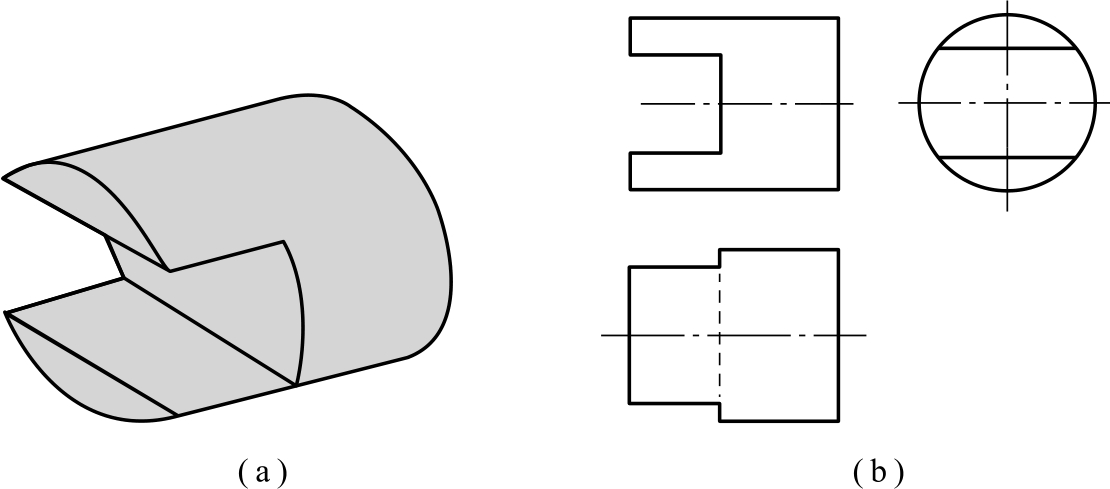
图2-69 圆柱开槽
(a)立体图;(b)三视图

圆柱开槽
![]()
如图2-70所示,求作切肩圆筒的俯视图。
切割空心圆柱和切割实体圆柱在原理上是一样的,切割空心圆柱可以看作是一个截平面同时切割了两个圆柱,同时要考虑圆柱空心的特点。
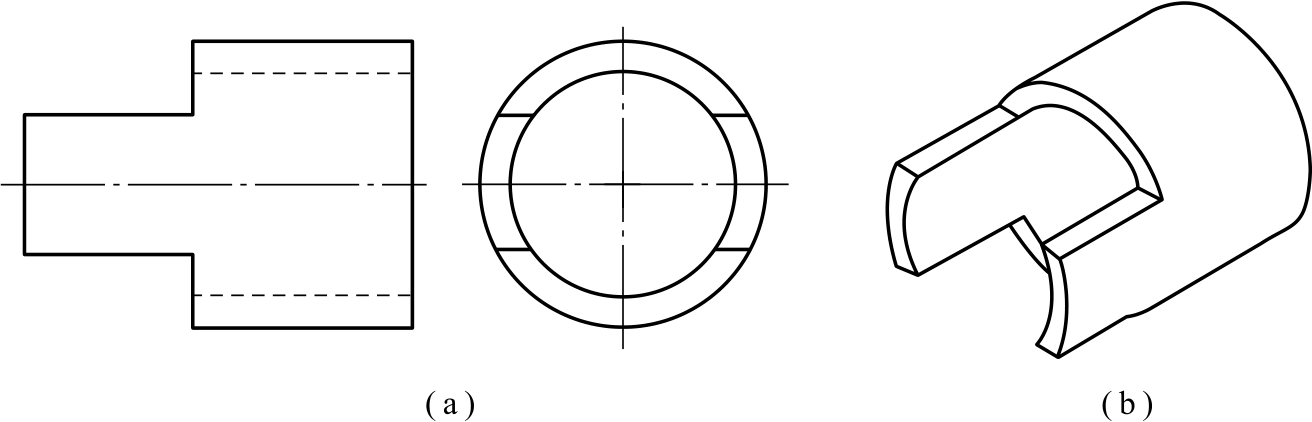
图2-70 切肩圆筒
(a)主视图及左视图;(b)立体图
