任务5 绘制圆球的三视图
![]()
如图2-54所示球体的直径为15,请绘制其三视图。

根据图2-55可知,球的任何投影都是圆。想一想,V面、H面、W面三个面投影的圆含义一样吗?为什么?
图2-54 球的立体图
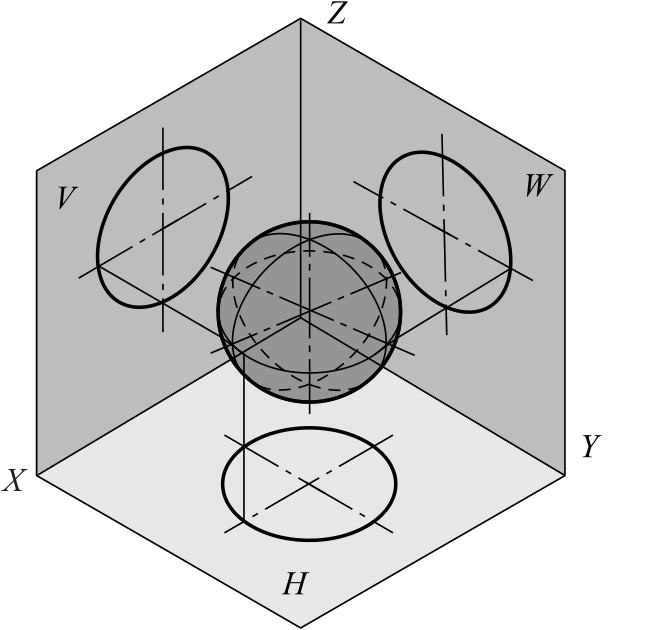
图2-55 球的三面投影图
![]()
一、圆球的形成
如图2-56所示,球面可看成是一个圆(母线)绕通过圆心的轴线旋转一周形成的。
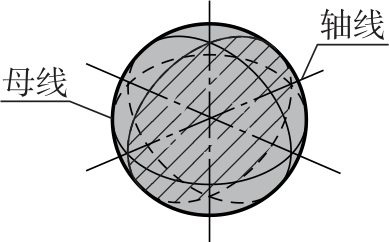
图2-56 球的形成
圆球面上有三个特殊位置的素线圆,分别是前、后半球分界圆,左、右半球分界圆,上、下半球分界圆。
前、后半球分界圆,可将圆球分为前后两部分;左、右半球分界圆,可将圆球分为左右两部分;上、下半球分界圆,可将圆球分为上下两部分。这三个特殊素线圆将圆球划为左前上区,右前上区、左前下区、右前下区、左后上区、右后上区、左后下区、右后下区八个象限区域。
将球分区,可以厘清球的空间形态,快捷便利地判断球表面的点或线的可见性,或者根据其投影的可见性判断其空间所在位置,有利于后期学习球的切割体。
二、分析球的投影特性
球的三面投影均为圆,但三个圆的含义却各不相同,如图2-57和图2-58所示。
(1)正面投影为圆,是前半球的投影,前半球的表面点的投影全部落在圆的内部,而所绘制的圆是前、后半球分界圆,对称中心线将球分为左前上区、右前上区、左前下区、右前下区;
(2)水平面投影为圆,是上半球的投影,上半球的表面点的投影全部落在圆的内部,而所绘制的圆是上、下半球分界圆,对称中心线将球分为左前上区、右前上区、左后上区、右后上区;
(3)侧面投影为圆,是左半球的投影,左半球的表面点的投影全部落在圆的内部,而所绘制的圆是左、右半球分界圆,对称中心线将球分为左前上区、左后上区、左前下区、左后下区。
半球的分界圆,在另外两个视图的投影,均积聚为一条线,且处于中心线位置。
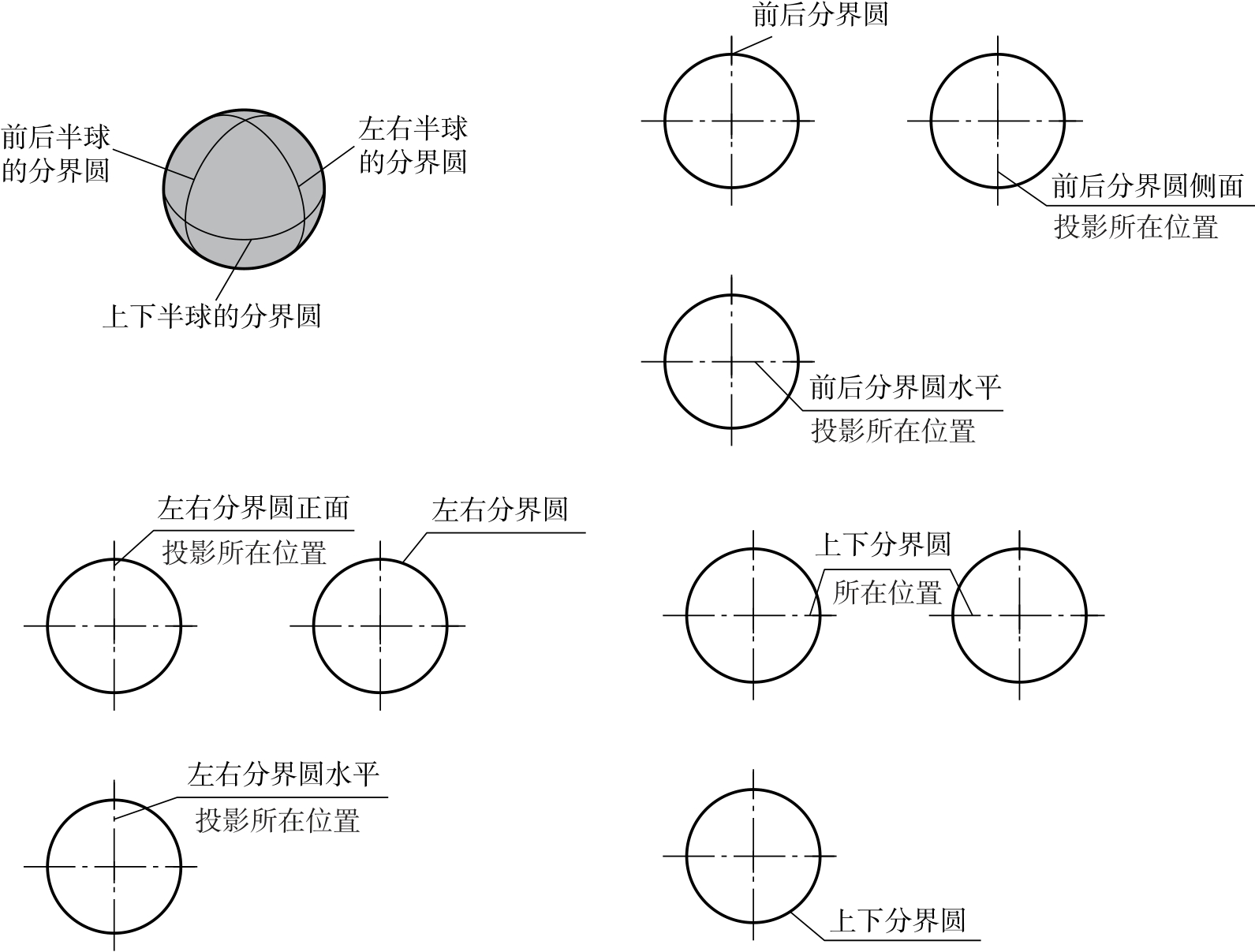
图2-57 球的投影分析
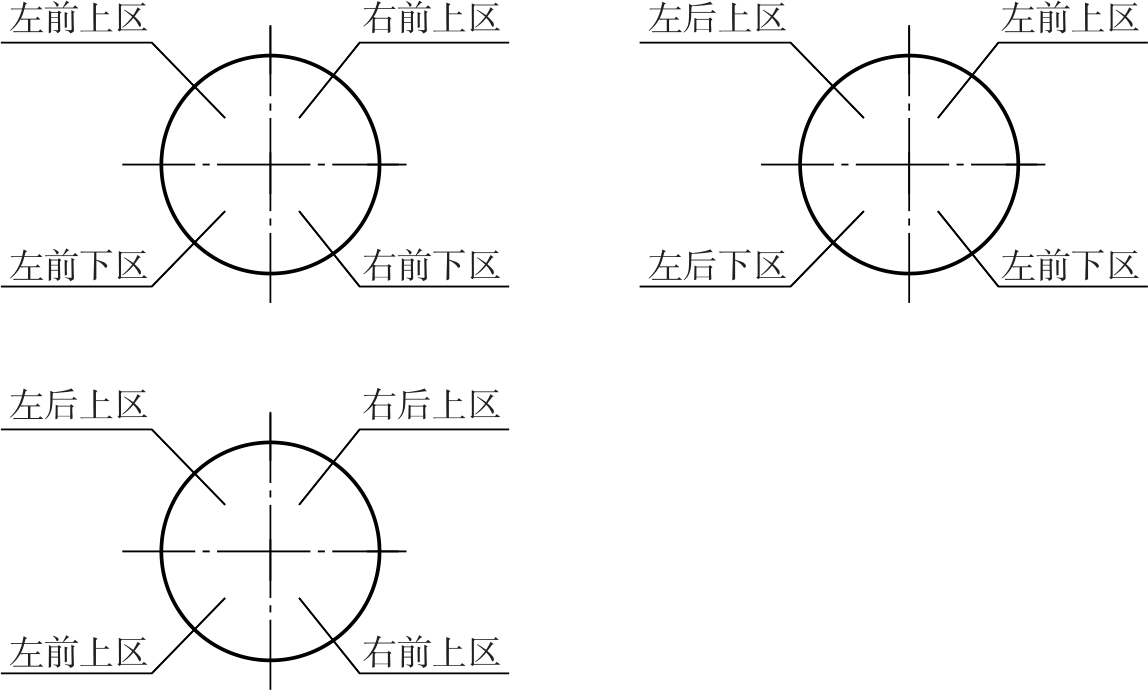
图2-58 球的分区
三、标注尺寸
确定球的大小只需要球的直径(小于半球的球体标注半径)。国家标准规定,在尺寸数字面前加注“Sϕ”或“SR”表示球的直径或半径,尺寸标注如图2-59所示。
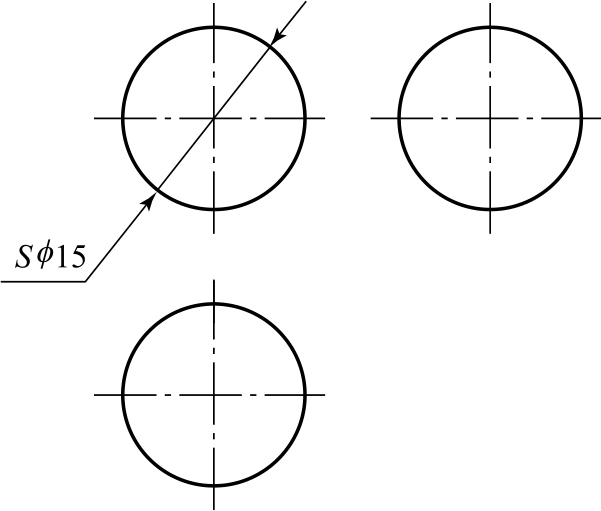
图2-59 球的尺寸标注
任务实施
该图绘制较简单,球的三面投影皆为直径为15的圆。
知识拓展
求球表面上点的投影
如图2-60所示,已知球面上点A的正面投影a′,下面求作其另外两面投影。
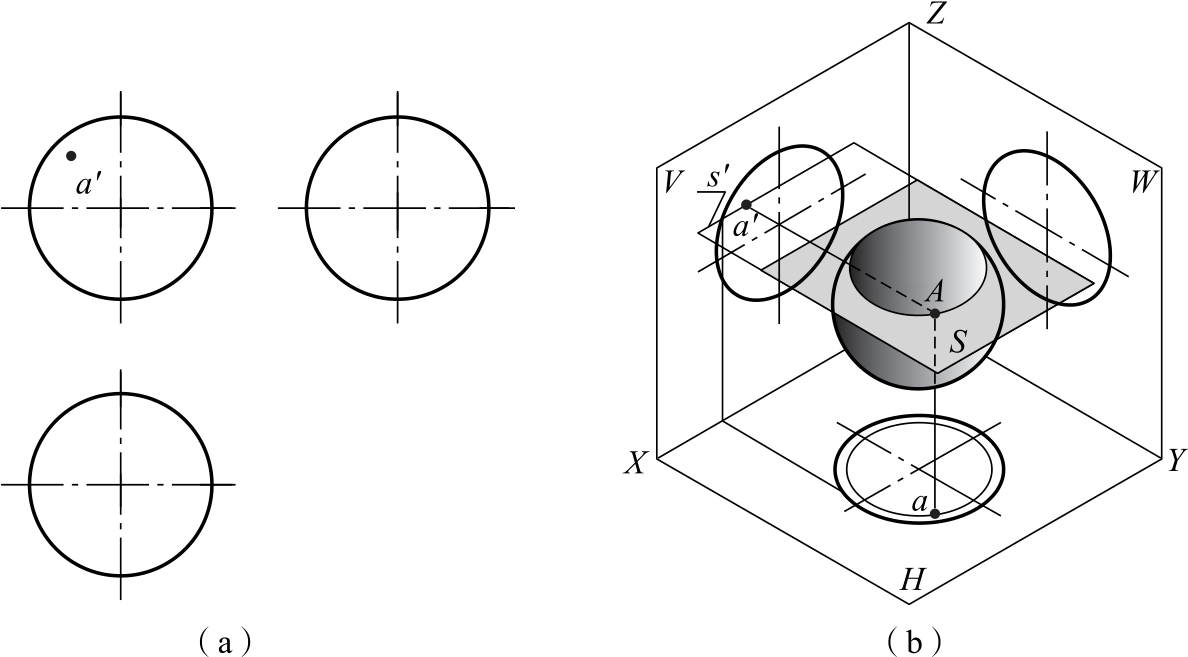
图2-60 求球面上点的投影
(a)三视图;(b)立体图
由于球面的任何投影都没有积聚性,球面的素线也不是直线,所以不能用前面求圆柱表面上点的投影的方法求球面上点的投影。
如果用平面切割球,得到的交线必定是圆,因此,可以用作辅助平面的方法,求球面上点的投影。如图2-60(b)所示,在求作点A的未知投影时,可过点A作水平辅助平面,具体作图步骤见表2-19。
这种利用辅助平面求点的投影的方法称为辅助平面法。
表2-19 求球面上点的投影的作图步骤
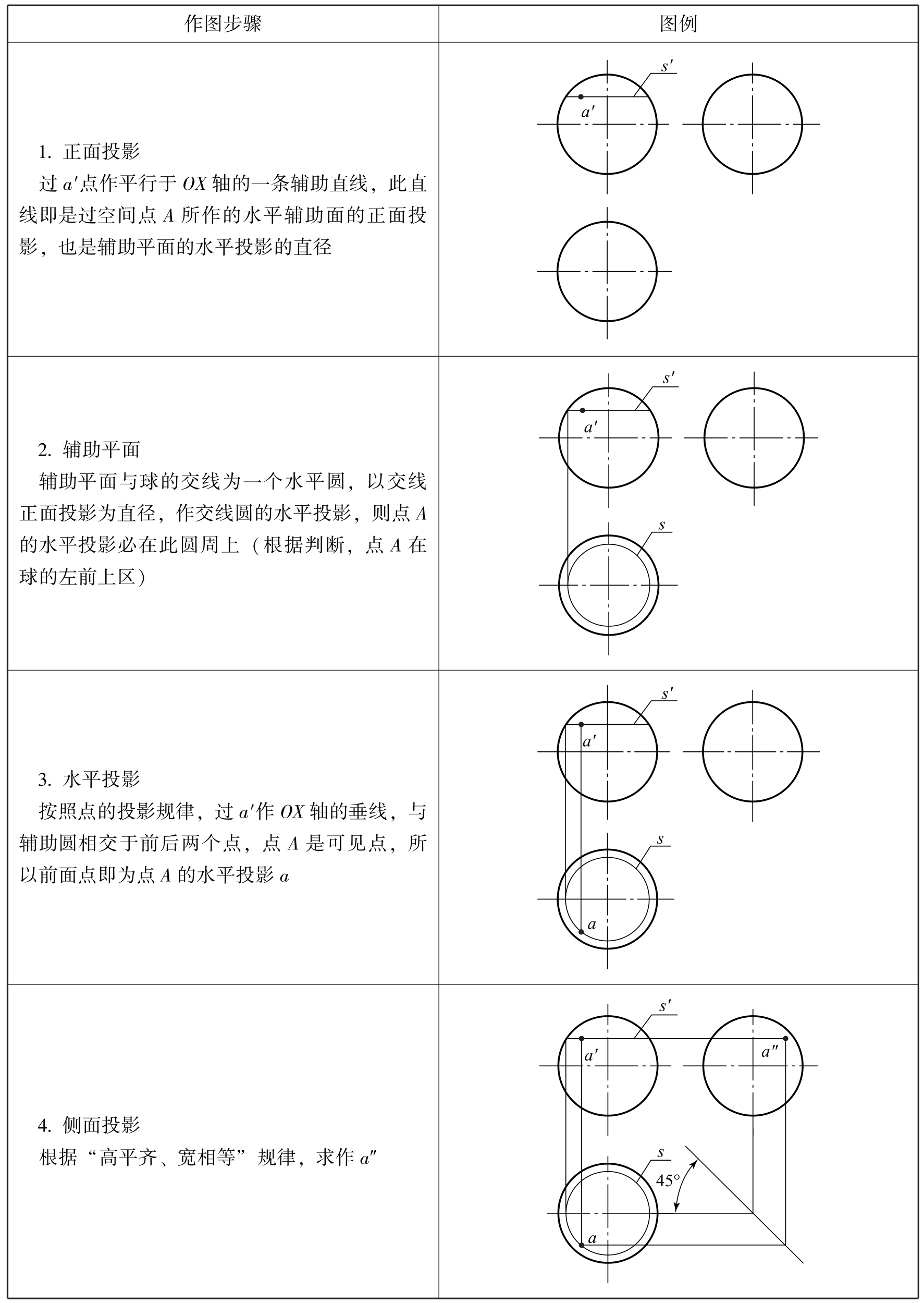
![]()
如图2-61所示,请思考一下,求出A、B两点的另外两面投影。
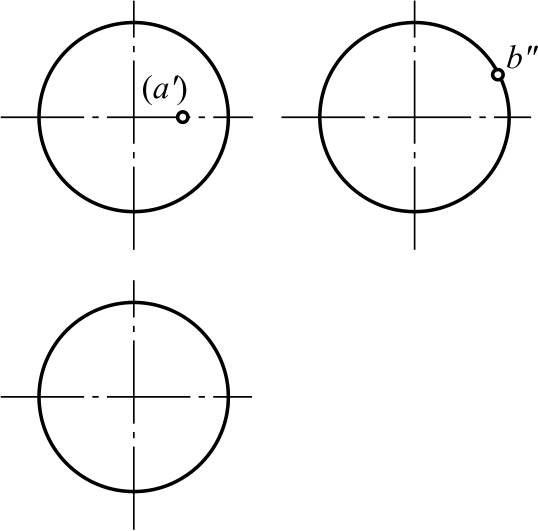
图2-61 求球面上点的投影
