任务1 绘制点的投影
![]()
如图2-17所示为长方体,将长方体放入三投影面体系中,试绘制长方体顶点A的三面投影。

若求A点的投影,需将顶点A向三投影面作垂线,垂足即是点A的投影,想一想:点A的三面投影与长方体的其余顶点有什么关系?点A的三个投影之间又有什么位置关系呢?
将A点向正投影面(V)投影,得到点的正面投影a′;将A点向水平投影面(H)投影,得到点的水平投影a;将A点向侧投影面(W)投影,得到点的侧面投影a″。将图2-12(a)所示的三投影面体系展开,即可得点的三面投影图2-17。那么,a,a′,a″分别与长方体的什么尺寸有关?
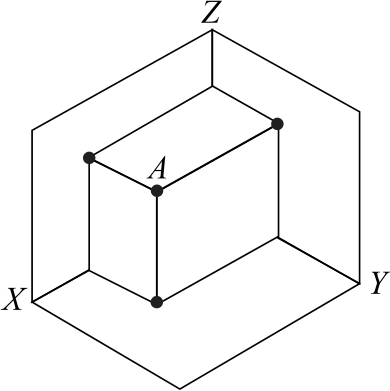
图2-17 长方体顶点的投影
![]()
一、点的投影及其投影规律
1.点的投影
由空间点A分别作垂直于H面、V面和W面的垂线,其垂足a、a′、a″即为点A在H面、V面和W面上的投影,如图2-18(a)所示。
2.点的标记
三投影体系中点的标记,遵循下列规定,如图2-18(a)所示。
(1)空间点 用大写字母表示,如A、B、M、N等;
(2)点的水平投影 用相应的小写字母表示,如a、b、m、n等;
(3)点的正面投影 用相应的小写字母加一撇表示,如a′、b′、m′、n′等;
(4)点的侧面投影 用相应的小写字母加两撇表示,如a″、b″、m″、n″等。
3.点的投影规律
将点A的三个投影a、a′、a″分别向X轴、Y轴、Z轴作垂线,垂足ax、ay、az必会重合。由此可知,点A和它的三面投影a、a′、a″,加上三个垂足ax、ay、az,再加上原点O,八个点正好组成一个长方体,如图2-18(b)所示。
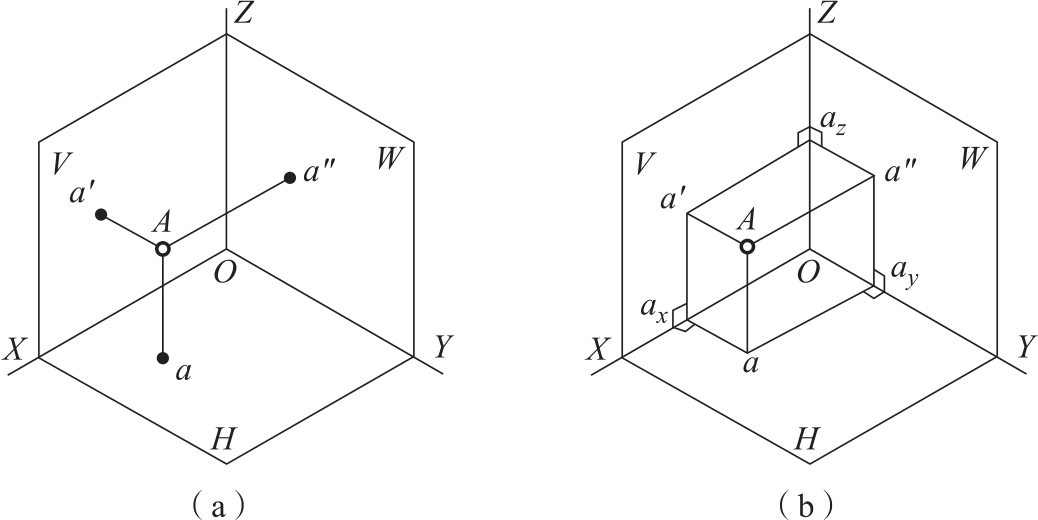
图2-18 长方体顶点的投影
此时,将三个投影面展开,可得点A的三视图,如图2-19所示,很显然,点的投影符合三视图的投影规律,由此可得到点的投影规律:
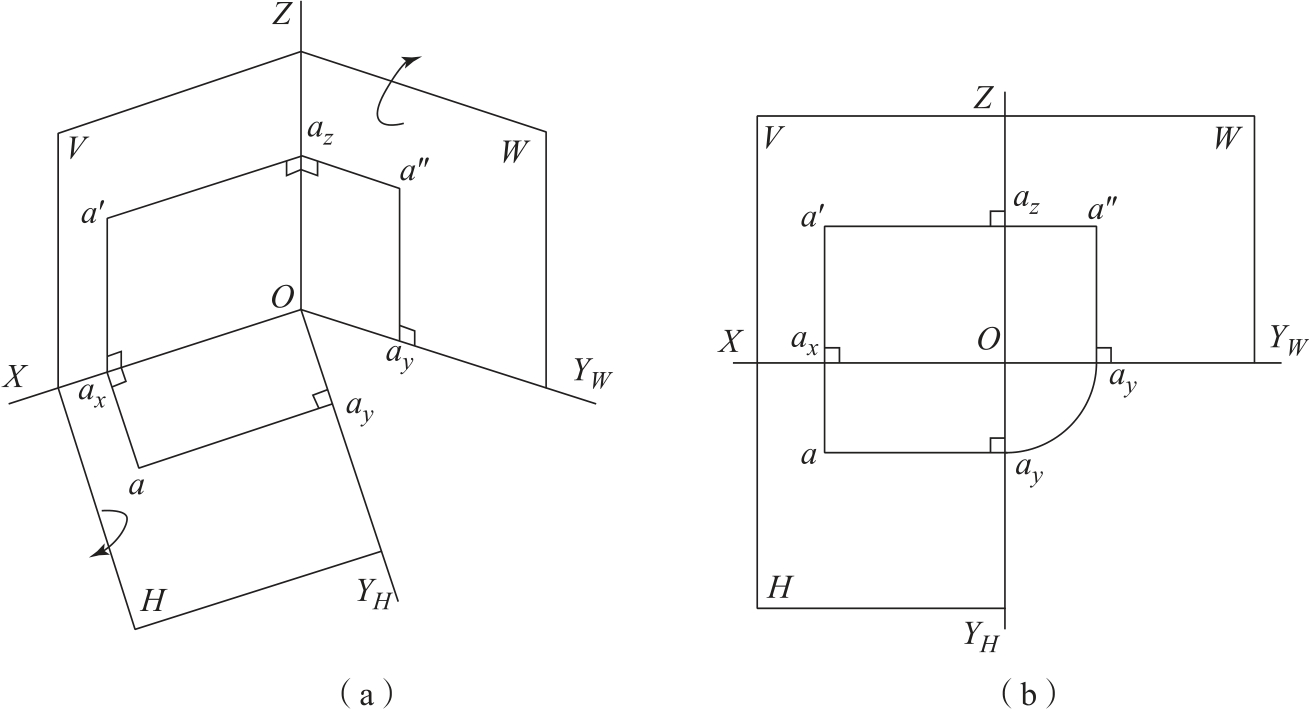
图2-19 点的投影的展开
(1)点的正面投影和水平投影的连线垂直于OX轴,即a′a⊥OX,即“长对正”;
(2)点的正面投影和侧面投影的连线垂直于OZ轴,即a′a″⊥OZ,即“高平齐”;
(3)点的水平投影到OX轴的距离等于其侧面投影到OZ轴的距离,即aaX=a″aZ,即“宽相等”。
作图时,为了表示aaX=a″aZ的关系,常用过原点O,以Oay为半径画弧,把点的H面与W面投影联系起来。(https://www.daowen.com)
根据点的投影规律,可由点的坐标画出三面投影,也可根据点的两个投影作出第三投影。
二、点的投影与直角坐标的关系
三投影面体系可以看成是一个空间直角坐标系,因此可用直角坐标确定点的空间位置,投影面H、V、W作为坐标面,三条投影轴OX、OY、OZ作为坐标轴,三轴的交点O作为坐标原点。
由图2-18(b)可以看出,A点的三个投影与其直角坐标的关系:
(1)点A到W面的距离Aa″=OaX=a′aZ=aay=x坐标;
(2)点A到V面的距离Aa′=Oay=aaX=a″aZ=y坐标;
(3)点A到H面的距离Aa=OaZ=a′aX=a″ay=z坐标。
所以点A的空间位置,可以用三个坐标来表示,写成A(x,y,z)的形式。点A每一个投影面的投影,可以用两个坐标来决定位置,如图2-20所示。
(1)正面投影a′,由坐标x和z决定;
(2)水平投影a,由坐标x和y决定;
(3)侧面投影a″,由坐标y和z决定。
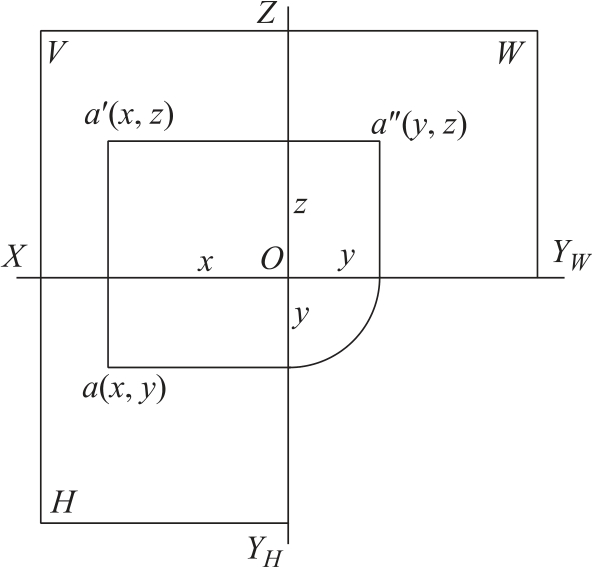
图2-20 点的投影与坐标的关系
任务实施
一、作长方体顶点的三面投影图
长方体顶点投影的作图步骤见表2-3。

点的投影
表2-3 长方体顶点投影的作图步骤
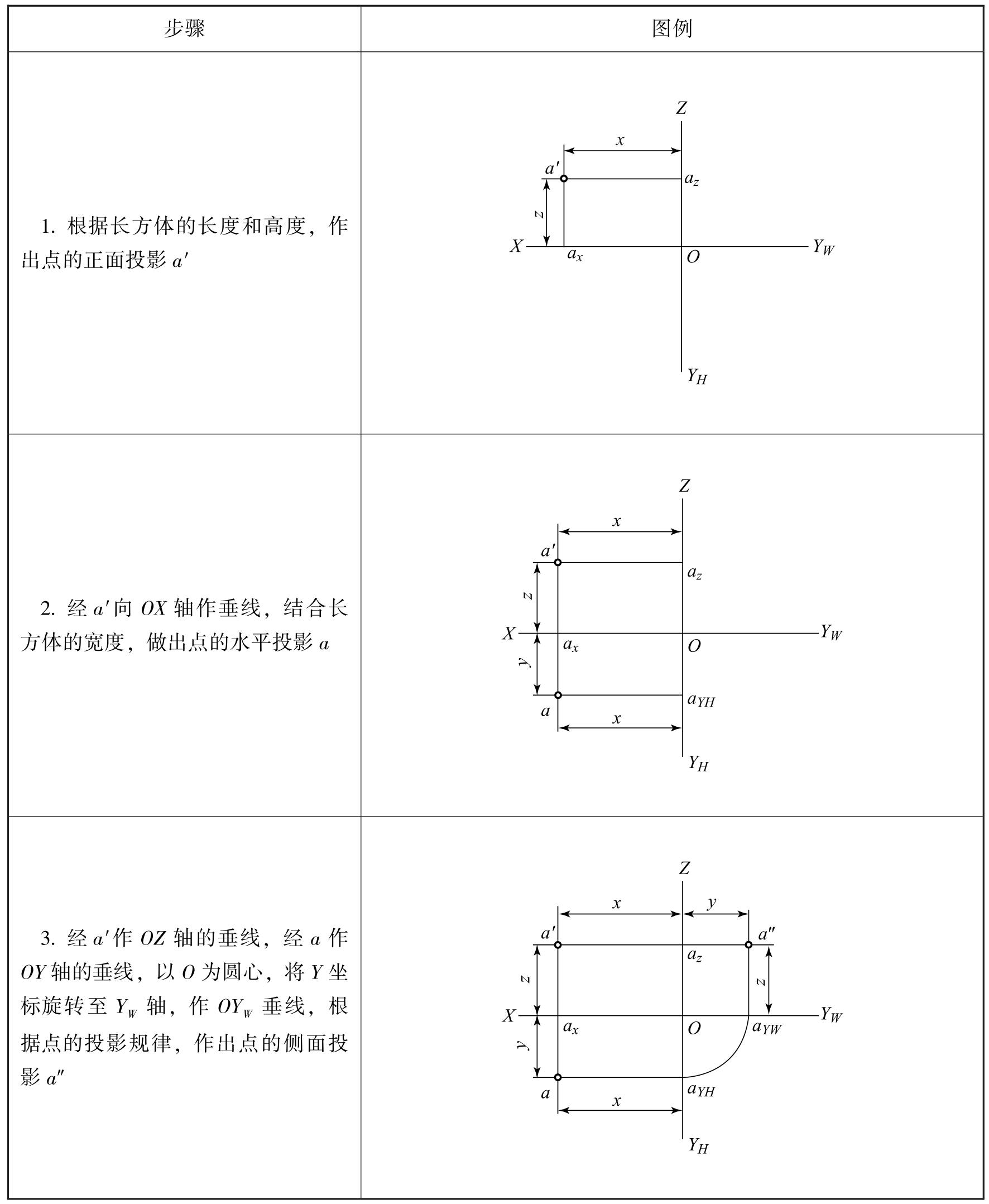
![]()
重影点的概念
在图2-21中,点A和点C的水平投影重合,该两点称为H面的重影点。点A和点C向水平投影面投射时,C点在上,先投射C点,A点在下,后投射A点,则认为C点是可见的,A点不可见,不可见点的投影,标记需加括号,如(a)。
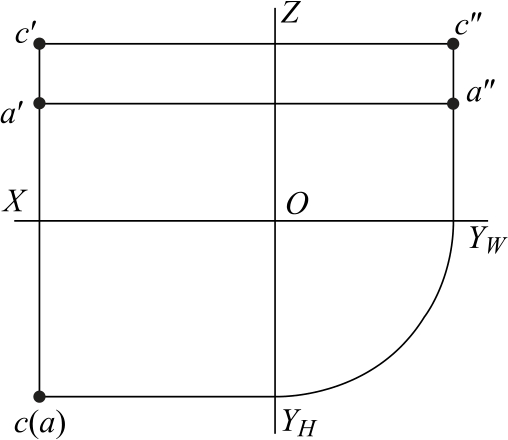
图2-21 重影点
![]()
如图2-22所示,已知E点的两面投影,求作第三面投影。
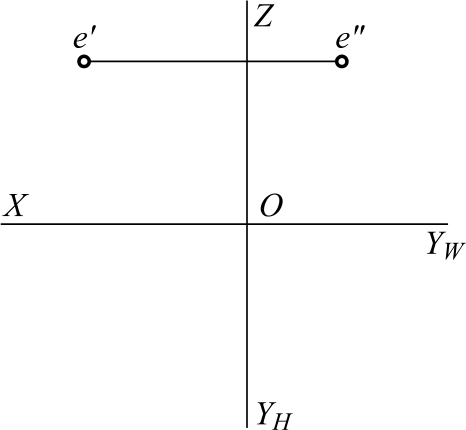
图2-22 已知点的两面投影求第三面投影
