任务 绘制正交两圆柱的相贯线
![]()
两圆柱正交相贯,其三视图如图2-75所示,试补画主视图上相贯线的投影。
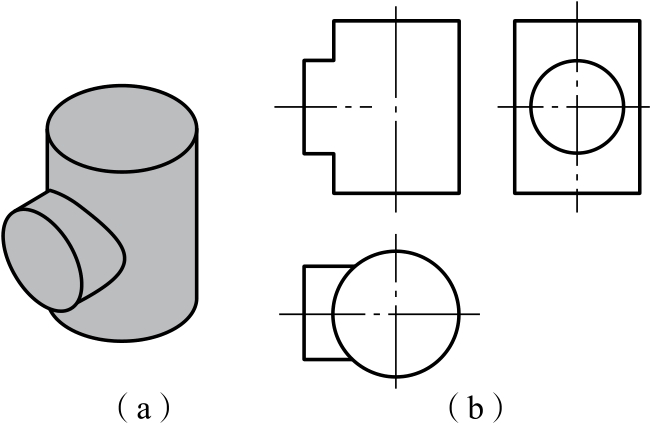
图2-75 两圆柱正交相贯线
(a)立体图;(b)三视图

如图2-75所示,两圆柱的交线是什么形状?交线的已知投影在哪个视图上?是什么形状?想象一下交线在主视图上的形状。
![]()
一、相贯线的概念基本特性
如图2-75所示为两圆柱正交相贯,两圆柱面相交产生了一条封闭的空间曲线,这种曲面体和曲面体因贯穿而产生的交线称为相贯线。
相贯线的形状多种多样,比较复杂,比如曲面体有圆柱、圆锥、圆球等不同形状,所以其相贯线形状各不相同。两个相贯的曲面体的直径有所变化时,也会影响相贯线的形状。两个相贯曲面体的轴线的相对位置及相对夹角发生变化时,同样会造成相贯线的形状发生变化,但不论形状怎么变化,相贯线均具有以下两个基本特性:
(1)封闭的空间曲线。不论是何种情况的相贯线,形状都是封闭的空间曲线。
(2)共有性。因为相贯线是两个曲面立体相交产生的,所以相贯线是两个曲面立体表面的共有线,相贯线上的点均为两立体表面的共有点,具备立体的所有投影特性。
二、两圆柱正交相贯的投影分析
(一)两实体圆柱相贯
相贯线的形状复杂多样,不便一一介绍,这里只介绍两圆柱正交产生的相贯线。
由图2-75(a)可知,因为两圆柱的轴线垂直相交(正交),所以在与圆柱轴线相垂直的投影面上,圆柱面的投影会积聚为圆,另两个投影面上,圆柱的投影为矩形。
相贯线(空间封闭曲线)是两圆柱面的交线,也是两圆柱面的共有线,因此同时具有两圆柱面的投影特性,即:相贯线的水平投影与大圆柱面的投影重合(为圆的一部分圆弧),相贯线的侧面投影与小圆柱的侧面投影重合(为整圆)。因此,该相贯线的水平投影和侧面投影是已知的,而其正面投影则在两矩形框交汇处,需要根据求点的方法来一步步求得。
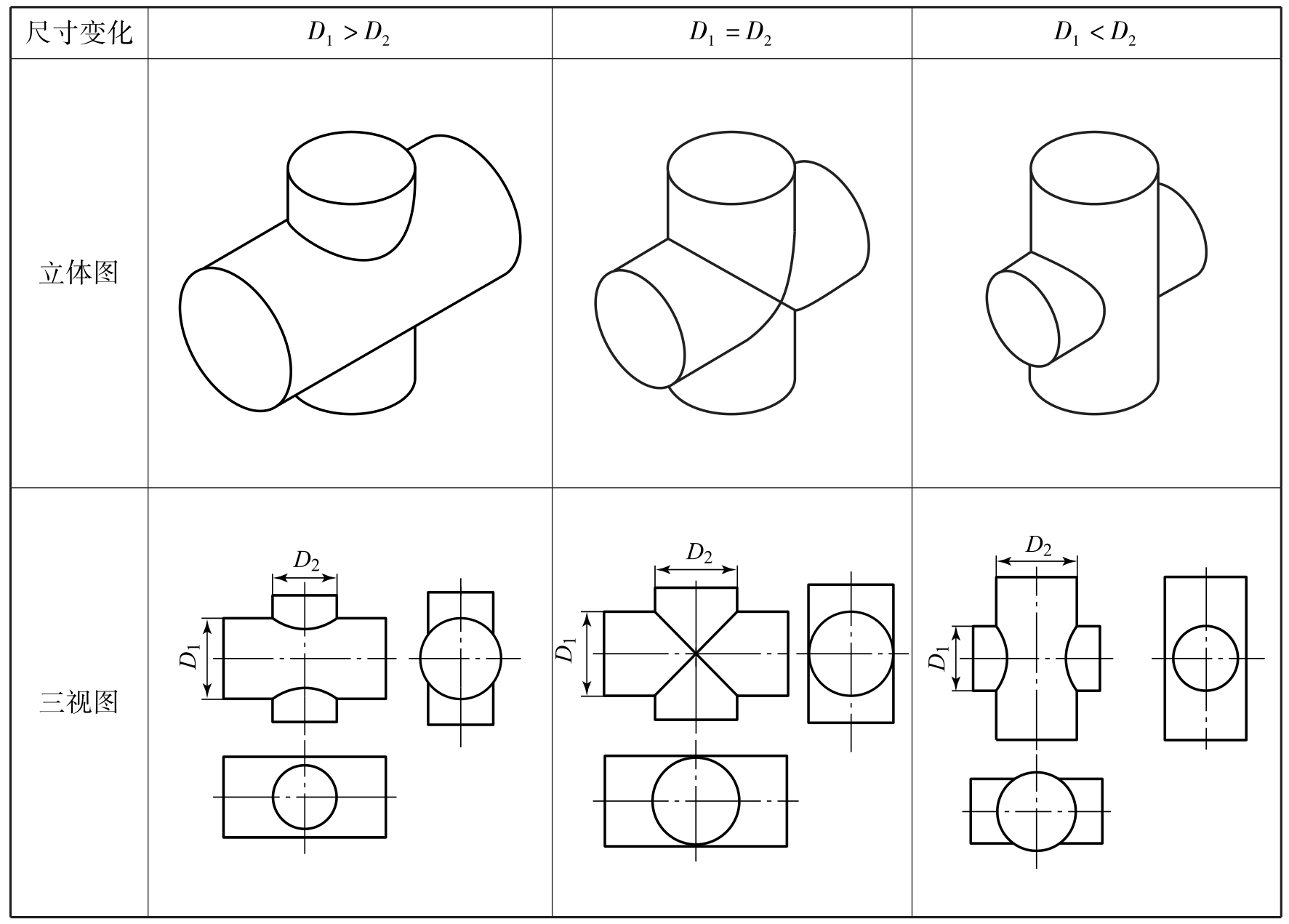
两圆柱直径不同,其正交产生的相贯线的形状也不相同。其变化规律如表2-28所示。特别注意的是:当两圆柱的直径相等时,其相贯线是两个平面椭圆且垂直相交。
表2-28 两圆柱正交相贯的相贯线
(二)两空心圆柱相贯
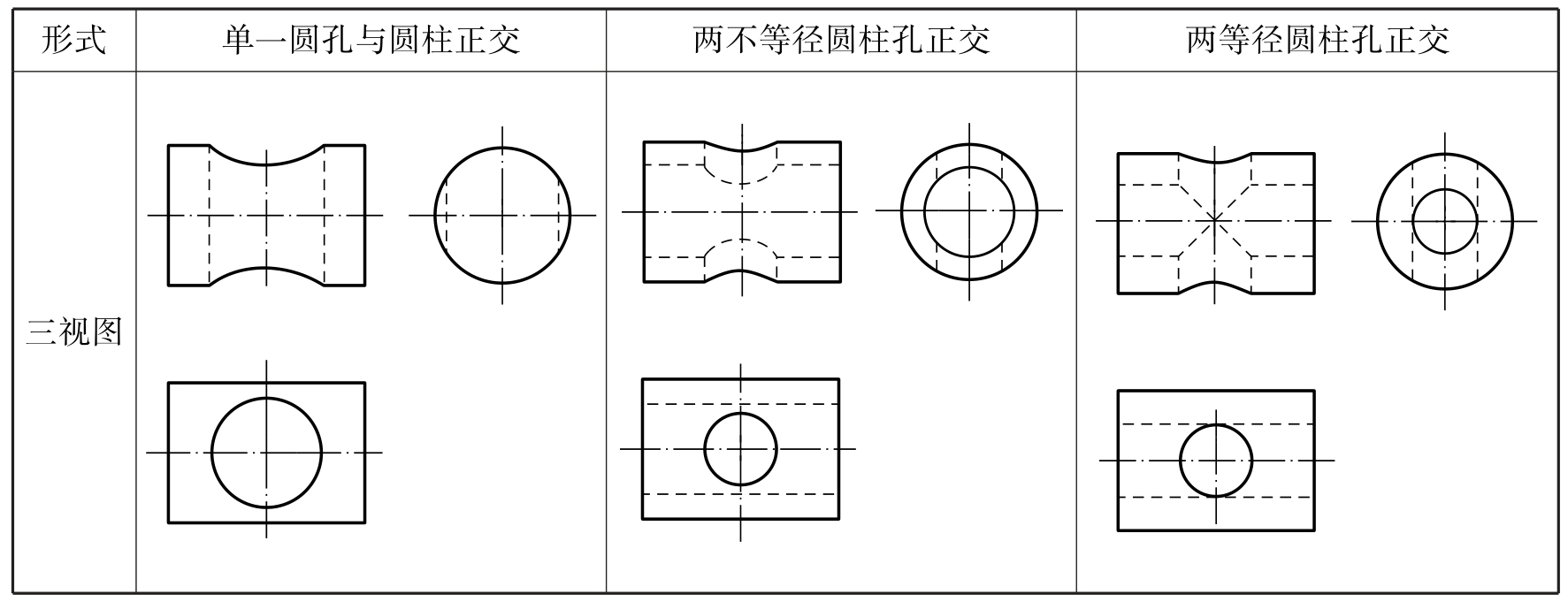
对于圆柱穿孔后的相贯线,和实体圆柱的相贯线是一样的,只是要画成虚线,如表2-29所示。
表2-29 圆柱穿孔的相贯线
(三)相贯线的特殊情况
1.相贯线为平面曲线
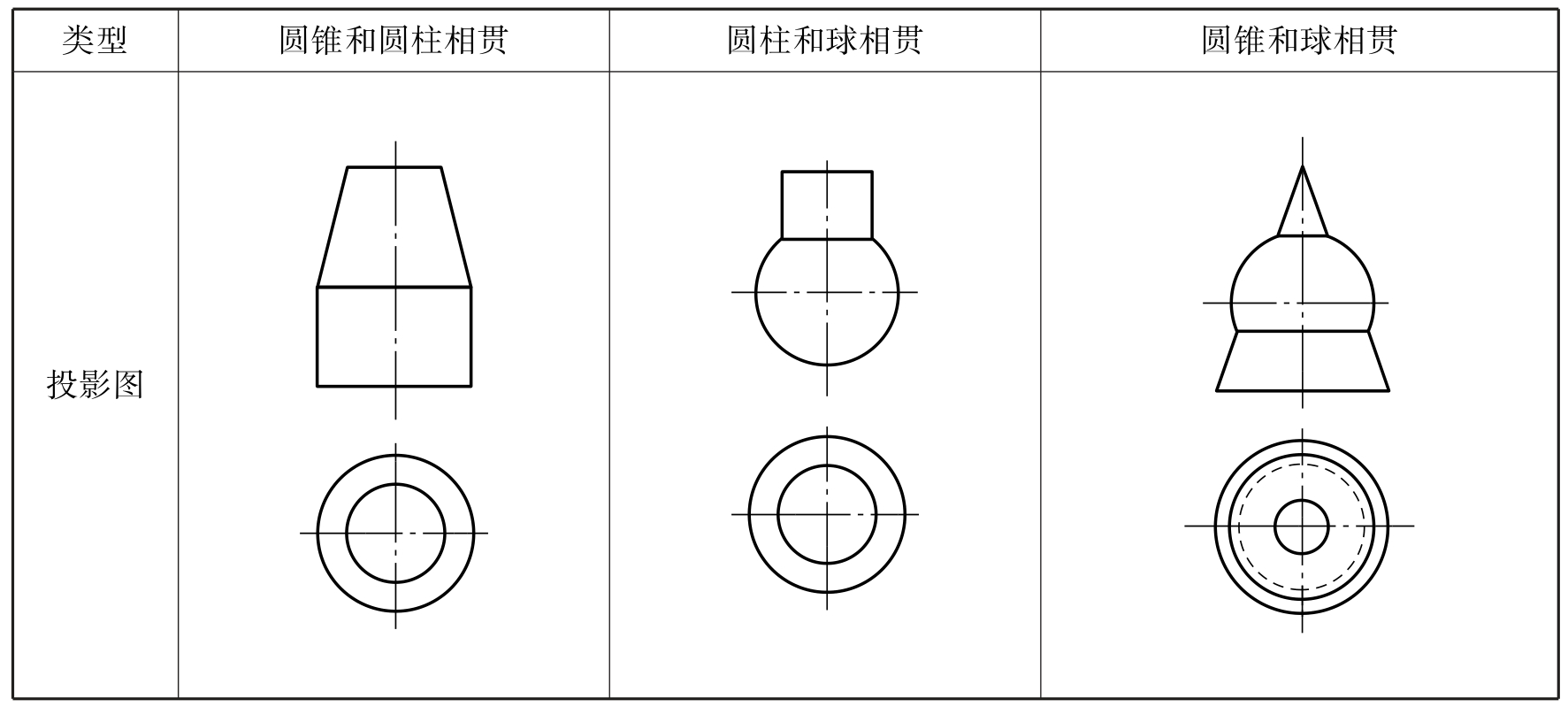
两个同轴回转体相交时,具有公共轴线,它们的相贯线一定是垂直于轴线的圆,当回转体轴线平行于某投影面时,这个圆在该投影面的投影为垂直于轴线的直线。见表2-30。(https://www.daowen.com)
表2-30 同轴回转体的相贯线——圆
2.相贯线为直线
当两圆柱面的轴线平行时,相贯线为直线。当两圆锥面共顶时,相贯线为直线,如图2-76和图2-77所示。
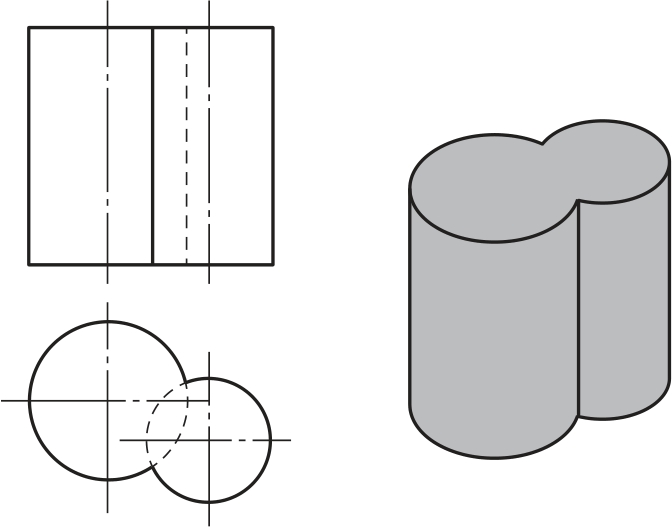
图2-76 相交两圆柱轴线平行的相贯线
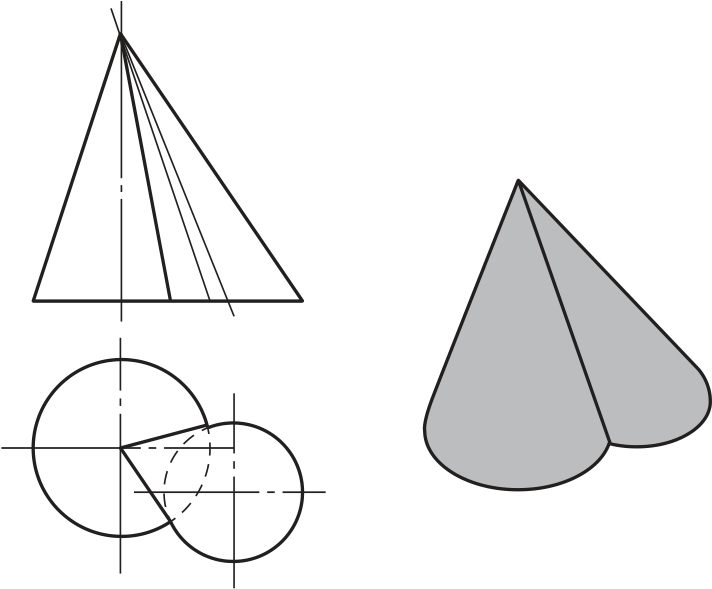
图2-77 相交两圆锥共顶的相贯线
三、两圆柱正交相贯线的投影作法
在绘制两圆柱正交相贯线时,可以依据下面方法求得。
(1)因为相贯线是两立体表面的共有线,所以其投影同时满足两个立体的投影特性,比如真实性、积聚性和类似性,所以绘制时,应根据两个立体的投影双向求证;
(2)绘制相贯线时,可先求点,再连点成线即可。对于两圆柱正交相贯,可以找出相贯线上的特殊位置点(即最高点、最低点、最前点、最后点、最左点、最右点),再在适当位置选取一般点,并根据点的投影规律求作未知投影,光滑连接各点即得相贯线的未知投影。
任务实施
两圆柱正交相贯线具体作图步骤见表2-31。

圆柱相贯
表2-31 绘制两圆柱正交相贯线的具体作图步骤
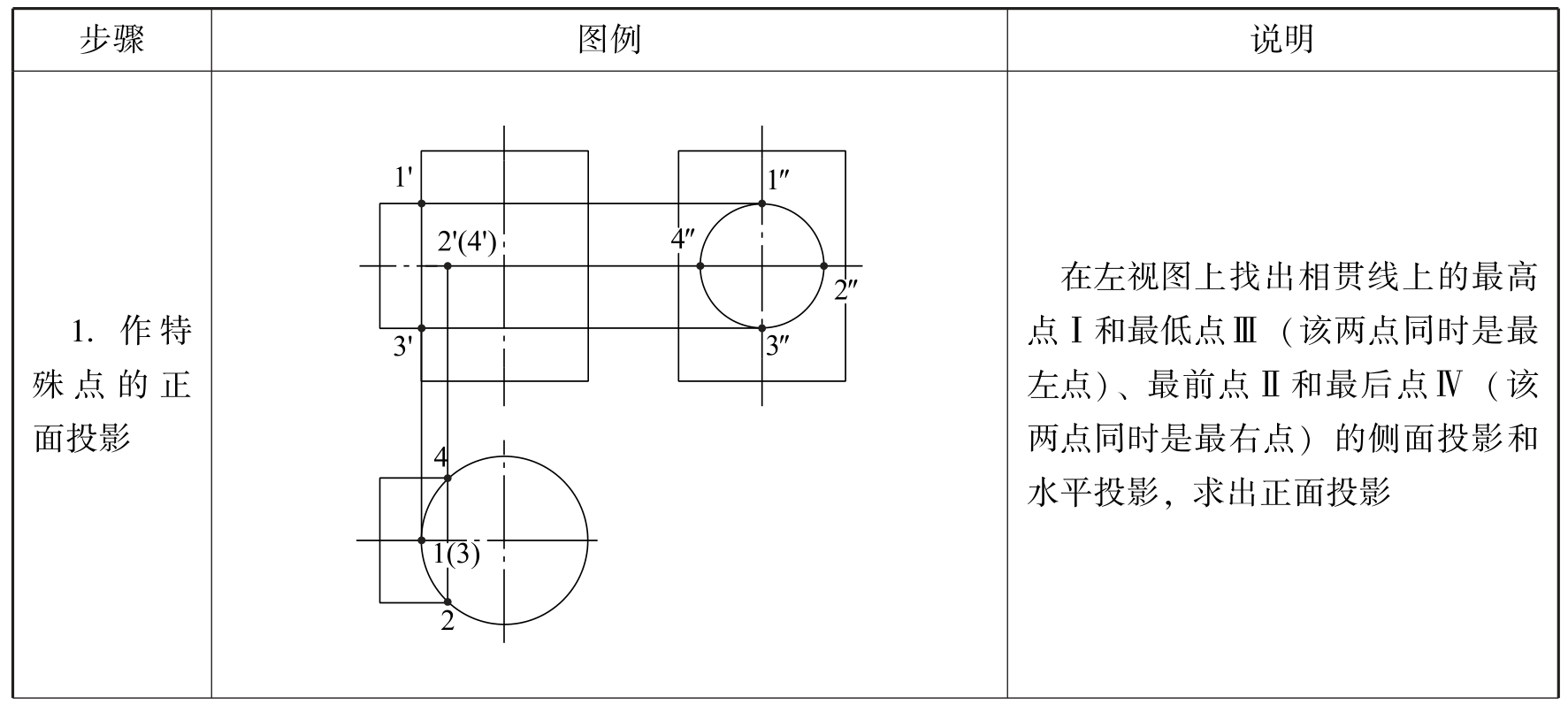
续表
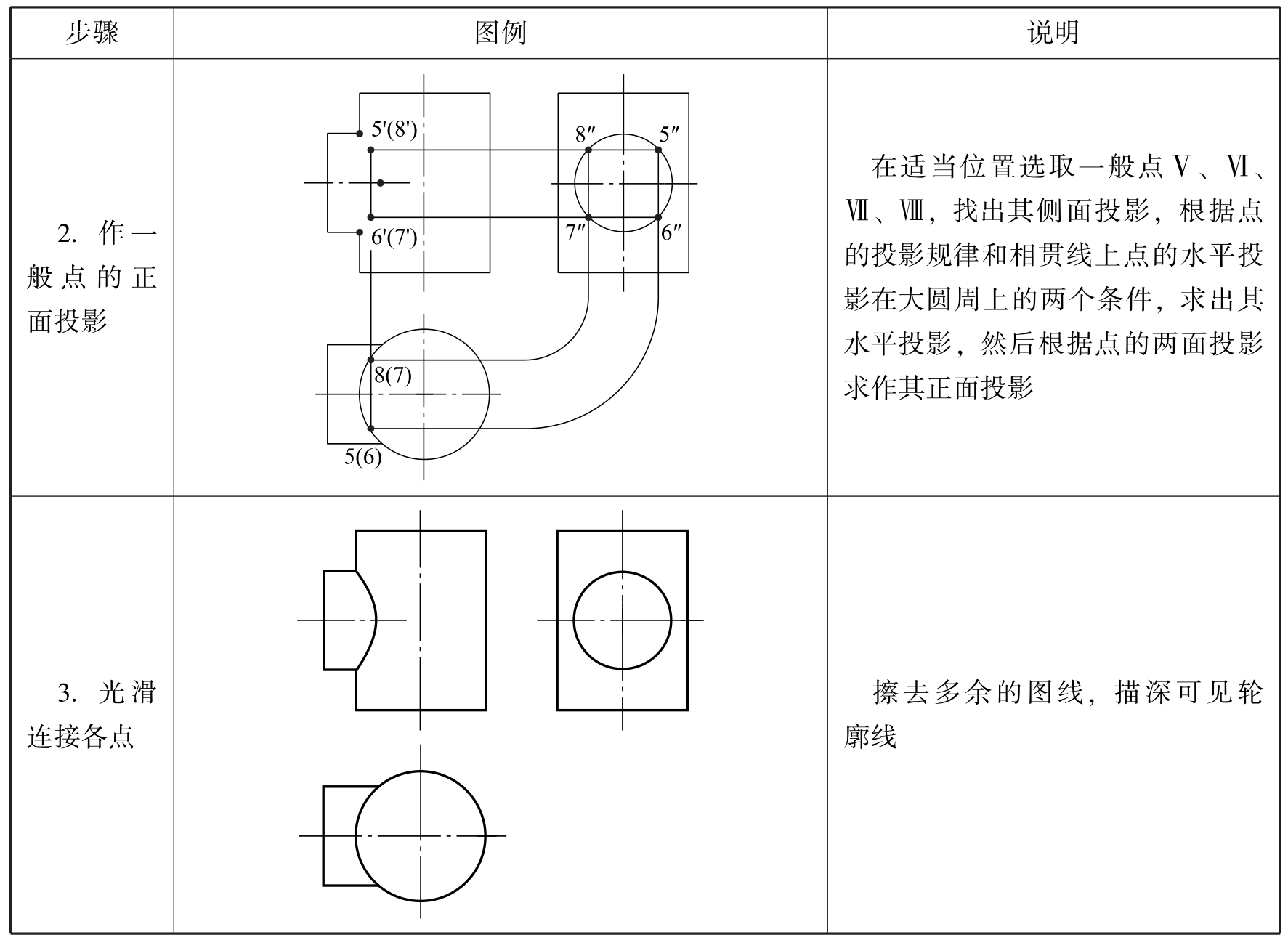
![]()
相贯线的投影作图
两回转体的相贯线,实际上是两回转体表面上一系列共有点的连线,求作共有点的方法通常采用表面取点法和辅助平面法。表面取点法就是取特殊点和一般点;辅助平面法就是在适当位置过两立体作一辅助平面。
![]()
请认真思考后补画出图2-78俯、左视图上的相贯线的正投影。
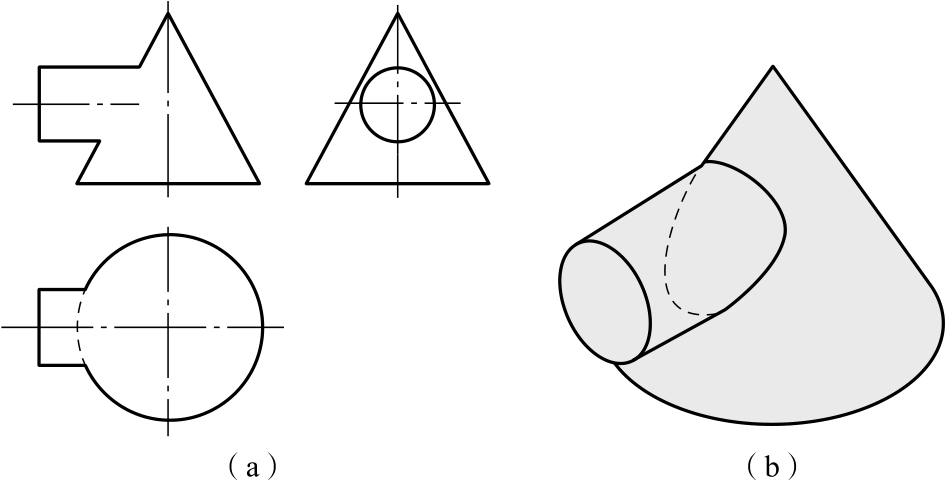
图2-78 补画相贯线
(a)三视图;(b)立体图
