人工神经网络简介
目前计算机的特点是串行计算,这也是它的一个缺点,使计算机无法很好地解决组合优化和模式识别等计算复杂度很高的问题。一个典型的组合优化问题是TSP(Traveling Salesman Problem):已知n个城市的分布或其距离矩阵,要求确定一条总路径最短的Hamilton回路,即遍历各城市当且仅当一次的最优回路。对于n个城市的平面TSP,剔除方向性,存在(n-1)!/2条不同的路径。若n=20,则存在1.2×1018条回路,即使每秒列举一亿条回路的计算也需350年,且随着城市数增加,计算量将超指数增长。数学和理论计算机科学已经证明TSP是NPC(非多项式完备)难题。鉴于其重要的工程与理论价值,TSP常作为算法性能研究的典型算例。
模式识别问题包括字符识别、手写体识别、语音识别、图像识别等。用常规算法来解决模式识别问题和组合优化问题类似,因为模式的不可穷尽性,也很困难。
为了解决这些难题,研究者尝试了很多其他方法,人工神经网络技术就是一个主要研究方向。它起源于人类对自身的思维器官——大脑的认识。
19世纪,生理学家发现了诸如感觉、视觉和肌肉运动等依赖于个体细胞的神经系统的宏观效应。这些细胞通过引发电流或对电流做出反应,从而能够接收和传送信号。显然,神经系统和大脑是自然界进化中的一种最为复杂的系统。人的大脑中至少有100亿个神经元(神经细胞)。每一个神经元均接受其他细胞的输入,并把输入整合起来,产生某种输出,同时将它送给其他神经元。输入由特定的突触所接收,输出由特定的输出线所发送,这种输出线叫作轴突。
人工神经网络理论(连接主义)来源于20世纪30年代的控制论和自组织理论的共同影响。瑞士学者进行了一项名为遗传认识论的研究工作,它被描述为演进式的认识论。同一时间美国的学者进行了实验认识论的研究。科学家将这种认识论的自然化称作控制论,该名字来源于Wiener。非常明确地说,控制论是一门关于思想和认识的自然科学。
代表这种思想的一个典型例子就是1943年发表的影响广泛而深远的论文《植根于神经活动中的一种逻辑运算》。该文一方面建议用逻辑学来帮助解释人脑及其思考和认知能力;另一方面将大脑看作这样一种装置,在它其中(就是在神经元中)蕴涵了逻辑运算。如图6-3所示,每个神经元被看作一个阈值元素,它可以是活跃的,或者是静止的,对应着逻辑值真或者假。多个神经元可以相互连接起来,这些连接对应于逻辑运算(与或非等)。在这种方式下,大脑就可以被看作一台机器。一个神经元在时刻n+1发放一个沿其轴突的脉冲y,如果在时刻n,它的输入X1,…,Xm和权重W1,…,Wm的权重和超过了神经元的阈值。有学者利用当时的真空管,构建了McCulloch-Pitts神经元网络。
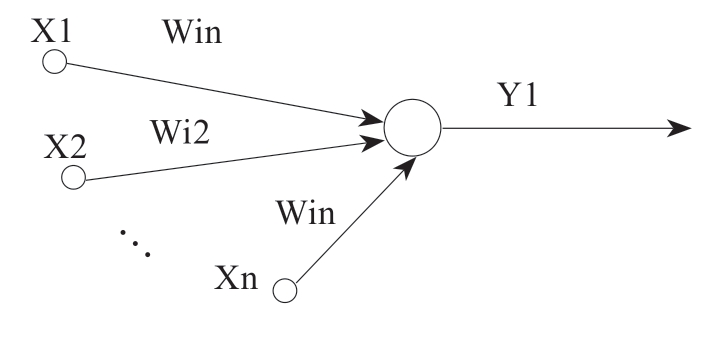
图6-3 McCulloch-Pitts神经元网络
McCulloch-Pitts神经元网络的一个缺点是节点之间连接权重的不变性。1949年,生理学家唐纳德·赫布(Donald O.Hebb)提出一种计算神经元之间连接强度的算法,后来被称为赫布规则。他强调,两个同时处于活动状态的神经元会加强它们之间的连接强度。
伯纳德·威德罗(Bernard Widrow)和特德霍夫(Ted Hoff)在1959年适应性线性网络研究中建议,计算每一个神经元的实际输出和理想输出之间的误差,然后将该误差向网络中传播,以便使得神经元之间的权重逐渐改变,直到输出误差最小为止。该规则被称为Widrow-Hoff规则。1958年罗森布拉特(F.Rosenblatt)设计了第一个人工神经元网络“感知机”,如图6-4所示。这个二层网络用来进行模式识别,如字符和语音识别。它通过一个有监督的学习过程进行学习。
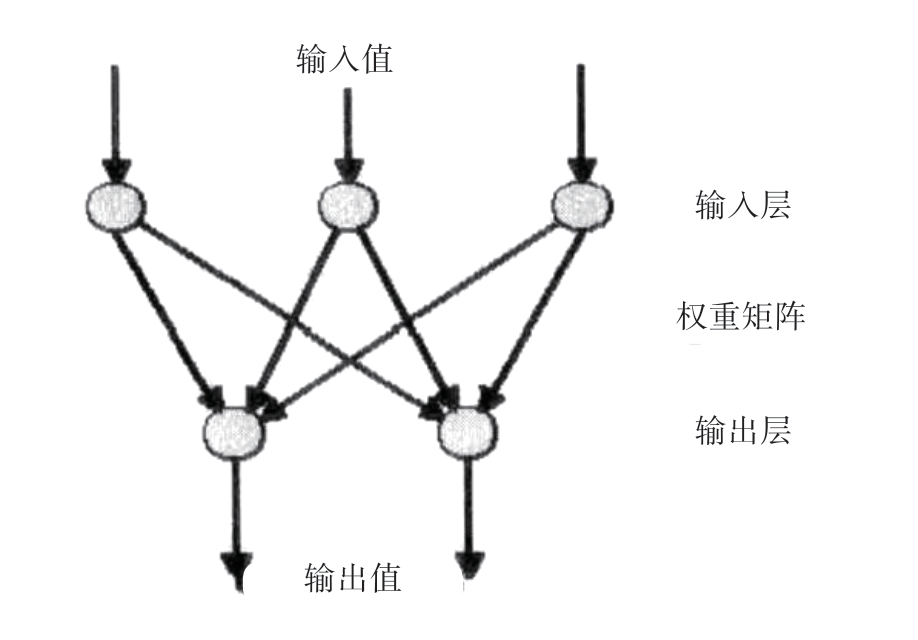
图6-4 二层感知机模型
20世纪50—60年代Von-Neumann计算机得到了飞速的发展,而神经网络方法则没有大的突破。1969年马文·明斯基(Marvin Minsky)和西蒙·派珀特(Seymour Papert)在他们的著作中对感知机模型提出质疑,因为它连简单的逻辑运算如XOR问题都不能解决,对解决其他问题更缺乏有效的算法。由于马文·明斯基在计算机界的权威性,人工神经网络研究从此陷入了低谷。
直到1986年鲁梅尔哈特(Rumelhart)和迈克塞兰(McClelland)为多层网络设计了反向传播算法,如图6-5所示,这种算法具有较强的学习能力和较为广泛的应用前景,人工神经网络方法重新引起人们的重视。该算法是一个有监督的学习过程,权重计算按照Widrow-Hoff规则反复进行,直到实际输出和理想输出的误差足够小为止。这种反向传播算法被广泛应用在分类、模式识别、数据分析等方面。
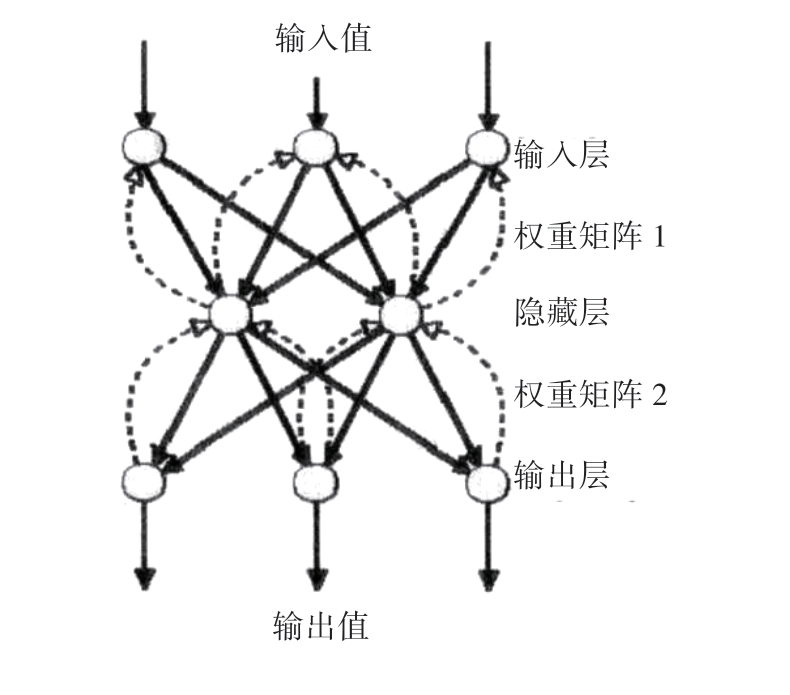
图6-5 反向传播网络(BP网络)
当人们沿着心理学、生理学路线研究神经网络的时候,物理学家霍普菲尔德在1982年设计了一个单层神经网络,如图6-6所示,其思想来源于电磁学上的自组织理论。这种网络的贡献有两个方面:一是网络的设计,神经元之间的权重变化使得一个局部的能量最小值可以得到,它可以被Lyapunov函数所描述,被一个非线性微分方程所计算;二是由现有的电子元件组成的神经网络硬件的实现,并使用该硬件计算出了30个城市的TSP问题的较优解。这一点非常重要,因为用硬件解决TSP问题的办法和传统的基于串行计算机的算法迥然不同。这种网络模拟我们至今所认识的人类大脑的结构和原理。如果能够真正在硬件上实现的话,它的运算能力就会更加充分地表现出来。
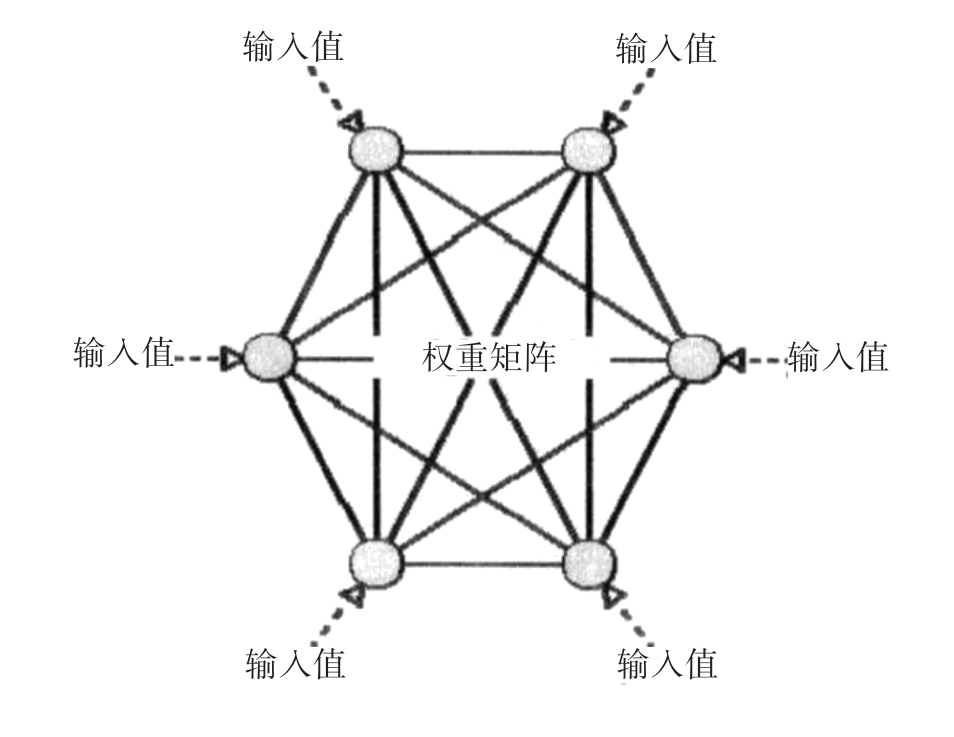
图6-6 Hopfield网络
这种网络的缺点是网络在演变过程中,经常陷于能量的局部极小点,而无法逃逸出去,无法达到全局最优解。因此,1985年提出了一个寻找全局最优解的方法,被称作模拟退火方法。或强或弱的震动改变网络在某个局部极小值停留的概率,就好像在气体中分子碰撞受到压力和温度改变的影响,这种概率型的网络被命名为玻尔兹曼(Boltzmann)机。玻尔兹曼是统计力学和热力学的奠基人。
芬兰物理学家和神经生理学家沃·科霍宁托伊(Teuvo Kohonen)在1982年开始研究更加接近生物大脑的网络模型和学习算法,被人们称作Kohonen网络(自组织图)。在神经网络分层上可以观察到聚类现象。外界因素的影响通过一个神经元层得到反映,在这个层次的学习过程中,一个反映外部影响的拓扑图被建立起来。这个学习过程被理解为神经网络的自组织过程,如图6-7所示。

图6-7 Kohonen网络(自组织图)
在神经网络的研究历史上,还有很多研究者做出了自己的贡献。例如,卡朋特和克罗斯伯格(Carpenter & Grossberg)于1987年提出的自适应谐振理论(Adaptive Resonance Theory,ART)等。
一个演示神经网络算法的综合系统是基于UNIX系统的SNNS。新版本的Java NNS则可以在Windows等系统上运行。随着人工神经网络的发展和普及,它的常用算法被包含在一些数理统计和分析软件中,如矩阵实验室(MATLAB)。
