习题2
2.1 有图2.21所示的二维稳态的对流-扩散问题，请用一阶迎风格式计算中心α点的变量φ。已知变量φ的控制方程为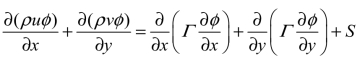
。式中ρ=1，Γ=1，S=10-4φ，流场速度u=5，v=3，网格距离Δx=Δy =1。
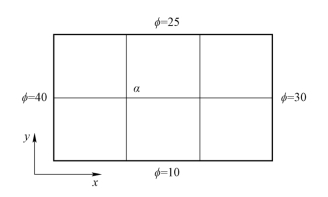
图2.21 二维稳态的对流-扩散问题
2.2 流速为u0=10 m/s沿正向的均匀流与位于原点的点涡叠加。已知驻点位于（0，-5），试求：（1）点涡的强度；（2）（0，5）点的流速以及通过驻点的流线方程。
2.3 平面势流由点源和点汇叠加而成，点源位于（-1，0），其流量为θ1=20 m3/s，点汇位于（2，0）点，其流量为θ2=40 m3/s，已知流体密度为ρ=1.8 kg/m3，流场中（0，0）点的压力为0，试求点（0，1）和（1，1）的流速和压力。
2.4 直径为2 m的圆柱体在水下深度为H=10 m以水平速度u0=10 m/s运动。试求：（1）A、B、C、D四点的绝对压力；（2）若圆柱体运动的同时还绕本身轴线以角速度60 r/min转动，试决定驻点的位置以及B、D两点的速度和压力。此时若水深增至100 m，求产生空泡时的速度（注：温度为15 ℃时，水的饱和蒸汽压力为2.332 × 103 N/m2）。
2.5 写出下列流动的复势：（1）u=U0 cos a，v=U0 sin a；（2）强度为m，位于（a，0）点的平面点源；（3）强度为Γ，位于原点的点涡；（4）强度为M，方向为a，位于原点的平面偶极。
2.6 介绍三种SIMPLE算法的改进算法，并说明其改进之处以及优缺点。
2.7 请对比结构网格与非结构网格的优缺点，并列出SIMPLE算法求解非结构网格的顺泰流畅的流程。
2.8 请给出雷诺方程的推导过程。
2.9 请列举出三种RANS方法运用的湍流模型，并简要说明这几种模型是如何处理雷诺应力的。
2.10 请给出k-ε模型和k-ω模型的控制方程组，并结合方程组比较二者所适用的情况。
2.11 请简要说明近壁面区域的流动特点，并说明k-ε模型和k-ω模型是如何处理近壁面区域的流动的。
2.12 请简要介绍y+的含义，并简要介绍如何通过y+得到近壁面网格的厚度。
2.13 请针对可压缩流体的二维管道流动，写出运用RNGk-ε模型计算该流场的控制方程，并说明用数值方法求解该控制方程的流程。管道和流场的参数可自行选取。