9.3.1 无人机的匀速追踪着陆过程
导引方法是制导系统控制导弹所遵循的规律,又称制导规律,它根据导弹和目标之间的相对运动信息(如视线角速度、相对速度等)形成制导指令,使导弹按一定的飞行轨迹攻击目标。20世纪40年代,美国就开始研究导弹的平面拦截。至50年代,已经研究出形式简单、易于应用的经典导引律,如比例导引法、追踪法、平行接近法等。随着目标机动能力的提高,传统导引律拦截来袭目标的精度逐渐下降,同时作战对脱靶量、能量消耗、过载等指标要求不断提高。伴随着现代控制理论和智能控制技术的发展,70年代以来,基于线性化模型的现代制导律逐渐诞生,这些导引律不仅能对付经典比例导引律很难精确应对的大型机动目标,而且拦截过程中能保证一些其他优良特性,如抗干扰、具有末端攻击角度约束、过载最小等。平行接近法是在导弹制导中运用的一种经典制导方法,是指在导弹接近目标的过程中,目标视线在空间始终保持平行,这种方法对导弹的机动性的要求较小,但是需要导弹目标及导弹的速度和前置角,并严格保持平行接近法的导引关系,这对导引系统提出了很高的要求,难度较大。平行接近法需要系统在制导的每一个瞬间,必须精确地测出弹体的速度、所需要的前置角以及目标的移动速度,而且要严格以平行接近法的导引准则来保持。采用平行接近法作为制导方法的导弹的飞行弹道相对平直,法向机动加速度也小于目标法向机动加速度,但是传统的平行接近法需要精确地测量目标任意时刻的速度的大小以及方向,因此准确测量所需要的信息成本和代价很高,这也是平行接近法在应用方面受到限制的原因,因此平行接近法并未得到广泛使用。但是这种导引方法已在基于视觉的追踪方面有所运用,因此在实现车载无人机精确着陆方面有一定的价值。
车载无人机的自主着陆,首先要实现无人机对于车辆的跟随。若车辆不在无人机机载云台相机的可视范围内,则需要通过DGPS提供的无人机以及车辆的信息来寻找车辆。这时候因为无人机距离车辆较远,因此可采用追踪法进行寻找,即无人机的速度向量水平方向的速度分量永远沿车辆到无人机的视线方向指向车辆。使用追踪法进行无人机对于车辆的寻找虽然相对比较费时间,但是可以在无人机捕捉到目标时,使无人机的速度方向和汽车的速度向量方向夹角较小。在无人机云台相机捕捉到目标之后,利用相机中目标的位置变化,可以计算得到车辆相对于无人机的速度矢量。当目标车辆与无人机的视线方向角达到一定数值之后,运用比例导引法进行无人机自主着陆。在无人机降落到一定高度时,控制无人机停止下落,进入精确着陆阶段。
所谓比例导引法,就是运用在导弹制导上的一种方法,其定义为:在导弹飞向目标的过程中,导弹速度向量的转动角速度与导弹指向目标的视线的转动角速度成比例。当无人机和车辆间的视线角随时间不变的情况下,这种方法又叫作平行接近法,此时无人机的运动可视为匀速运动,这种情况在无人机的高度足够高的时候是最理想的。
假设车辆在地面上匀速运动,并假设车辆在平地上行驶,则无人机在跟随车辆之后的着陆过程可以看作一个二维平面上的基于平行接近法的运动。如图9.3所示。
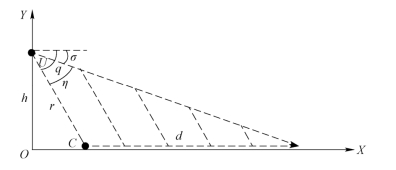
图9.3 车辆匀速运动过程中的追踪着陆过程
其中,X轴指向车辆运动方向,Y轴竖直向上,点C为车辆的位置,点U为无人机的位置,r为车辆到无人机的距离,h为无人机到标志物的铅垂距离。因为标志物位于车顶上,车顶具有一定的高度,因此h=hU-hC,其中,hU为无人机的绝对高度,hC为车辆的高度。d为直到着陆为止车辆所行驶的距离,q为目标线与基准线之间的夹角,σ为无人机速度矢量与基准线之间的夹角,η为无人机速度矢量与目标线之间的夹角。因为无人机在自主着陆过程中,始终处在车辆的上方,因此这三个角没有正负。对于比例导引法,这些变量之间会有如下的关系:

式中,K为系数,它的积分形式为
![]() (https://www.daowen.com)
(https://www.daowen.com)
即无人机速度向量的角度变化与无人机相对于车辆的角度变化成正比,如果这两个角度变化为0,就成为图9.3的理想情况,也就是平行接近法。设汽车的速度为Cv,无人机的速度为vX,沿X轴方向的速度为vUX,沿Y轴方向的速度为vUY,则在理想的平行接近的情况下,有如下的关系式成立:
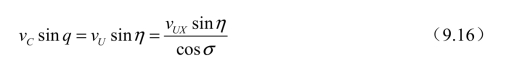
从而可以得到
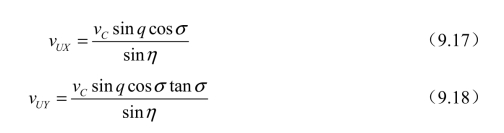
式中,q和Cv可以通过云台相机测量计算得出,在这种情况下η可以表示为η=q-σ。vUX受无人机最大飞行速度的限制,vUY受无人机最大下降速度的限制,可表示为
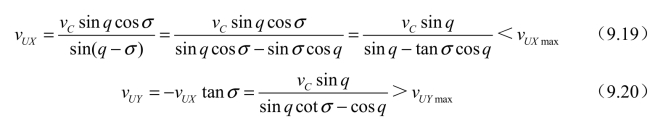
由式(9.19)可知,vC一定时σ与vUX、vUY的绝对值在σ的取值范围内呈正相关。假设车辆以vC=30km/h(8.3m/s)的速度行驶,视线角q=45°,则此时满足无人机最大飞行速度以及最大下降速度限制的σ值可以通过计算得到σ0=17.96°,此时车辆行驶过的路程为

假设无人机绝对高度hU=6m,按照一般轿车的平均高度hC=1.5m 计算,无人机的相对高度h=hU-hC 则可以初步判断上述情况下无人机着陆时车辆所行驶的距离l=9.37m。但此时无人机的下降速度vUY的值达到最快的4 m/s,即在1.125 s内完成着陆。这无疑将不利于四旋翼无人机自主着陆的安全性。为了保证无人机自主着陆的精确性,将无人机的降落时间定为3 s,即vUY =-1.5m/s,在视线角q=45°时,速度方向角经过计算得到σ=8.67°,无人机的水平方向的速度vUX =9.83m/s,此时车辆行驶的距离l=25m。
