4.3.1 锥形流场的生成
本节的锥形流场的生成是基于描述锥形流场的Taylor-Maccoll方程,通过求解0°攻角的锥形激波流场生成的。Taylor-Maccoll方程的锥形流场模型认为,无限长的锥形激波流场中特征长度没有意义,所以在激波面后任意一条从锥顶点发出的射线上,所有点的流动参数都是等值的,也就是说流场中的点的流动参数只与该点到锥顶点的连线与来流方向的夹角有关。马赫数在一定范围内的超声速来流使流场中形成了与圆锥同轴的一道圆锥形斜激波。圆锥形的斜激波与自由来流的倾角,处处相等。所以紧靠波后的流场参数均匀,激波强度不发生变化。Taylor-Maccoll方程的形式为
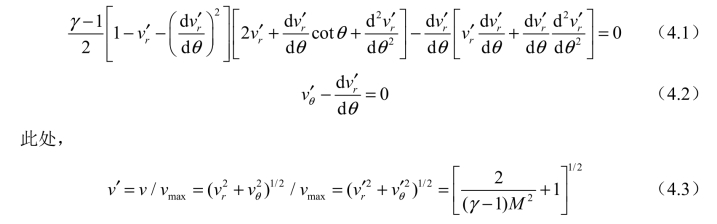
Taylor-Maccoll方程是一个常微分方程,存在解析解。因此可以从气流过激波面后的已知的流场参数出发,通过四阶Runge-Kutta算法对该常微分方程进行数值积分求解。Runge-Kutta法是计算常微分方程的一种迭代算法。其中,四阶Runge-Kutta法的精确度较高,经常运用在各类工程应用上。与常规的 Taylor-Maccoll方程对锥形流场的求解不同,在设计乘波体所需的基本流场中,生成流场的圆锥生成体的锥顶角对于圆锥流场的流动参数计算来说并不是必要的参数。因此可以通过直接给定激波角,代替通过锥顶角求得激波角的方式,通过数值方法计算激波后流场。其具体生成步骤如下。
(1)给出生成锥导乘波体的激波角β,设计条件的来流马赫数M1a、来流压力1p、温度1T。
(2)确定数值积分的角度步长。
(3)求解激波后参数初值条件:根据给定的波前参数通过斜激波前后的参数变化公式,可以计算得到紧邻激波面下游的波后流动参数。锥形流场每一条母线在紧邻激波面附近可视为斜激波。对于理想气体,斜激波激波面前后的各项流动参数对应关系式可以表示如下:
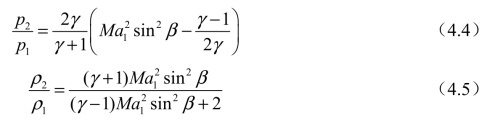 (https://www.daowen.com)
(https://www.daowen.com)
(4)从激波面出发,按照第(2)步确定的角度步长,以四阶Runge-Kutta法对Taylor-Maccoll方程进行迭代积分计算,直到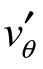 大于零时,停止计算。
大于零时,停止计算。
(5)由各个θ角微元处的流场速度参数,计算流场各点的密度ρ、温度T、压力p、马赫数Ma等其他参数。
求解的方程为
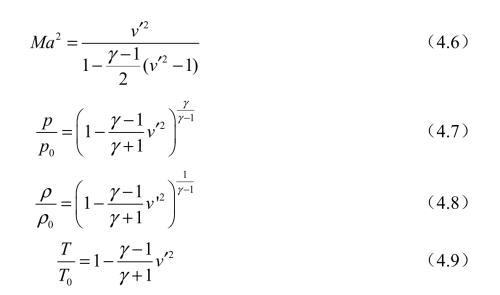
其中,压力p、密度ρ、温度T的求解需要激波后某点的相应数据。
用Matlab编写锥形流场生成程序,基于设计点β=12°,Ma∞=6,H=15km 的自由流场数据利用四阶Runge-Kutta法对Taylor-Maccoll方程进行求解得到锥形激波流场。
为了验证本章中采用算法的可靠性,本章以圆锥半顶角建立基础圆锥生成体,并对其划分网格,然后求解高超声速来流流经该圆锥生成体的无黏锥形流场。求解器选用基于密度求解器,气体模型设为理想气体,湍流模型使用无黏模型,对流项的空间离散格式采用Roe-FDS,迎风格式选用二阶迎风。在数值计算结束残差收敛后,从圆锥生成体的截面压强图中可以看出,压强等值线近似呈锥形,且锥顶点与圆锥生成体重合。可以测得最外侧的压强等值线锥的半顶角与通过生成体求得的激波角基本一致,误差不超过5%。这表明本章所使用的锥形流场生成方法、计算方法具有一定可行性。
