7.5　扑动飞行的尾迹涡街

帮助昆虫产生非定常高升力的机制，分别为“延迟失速机制”“旋转环流机制”“尾迹捕捉机制”和“Weis-Fogh拍合机制”，由于目前并没有具体的理论或者精确的经验公式来诠释低雷诺数下的空气动力学问题，这四种机制带来的升力效益一般来说仅仅可以估算。这些高升力机制可以通过对涡的分析得以体现。

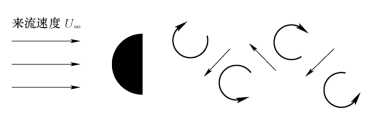
人们都知道的是，翼的扑动可以产生动力，同时在流场中产生一系列的涡。新的涡随着机翼扑动不断产生，随着来流向后漂移并不断变形，直到形成扑动稳定的尾迹涡街，简称尾涡，其结构和机翼的前飞状态息息相关，从尾涡可以直接看出机翼的扑动产生阻力还是推力。1935年Von Karman和Brugers表述了尾迹涡街里涡的位置、方向和其引发的阻力或者推力之间关系。他们将涡街里的涡分为上下两组，当上方涡均顺时针转动，同时下方涡逆时针转动时，观察尾涡中心，流场速度和来流相反，这说明半柱体对涡的作用和来流方向相反，施加给半柱体的力和来流方向相同，产生阻力，此时的涡街被定义为“卡门涡街”，如图7.8所示；当上方涡均逆时针转动，同时下方涡顺时针转动时，可以看出此时半柱体对涡的作用和来流方向相同，产生推力，此时涡街被定义为“反卡门涡街”（reverse Karman vortex street），如图7.9所示。

图7.8　圆柱绕流产生的卡门涡街

图7.9　翼扑动产生的反卡门涡街