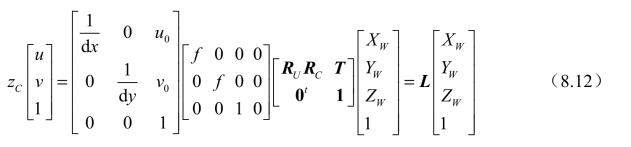8.3.1 几个视觉坐标系的转换
基于视觉的无人机导航运用的是计算机视觉中的方法。其中最主要的就是如何将2D的图像坐标信息转换成3D的图像坐标信息，其中涉及几个坐标系的转换。在无人机的视觉导航中常用的坐标系为图像坐标系、相机坐标系与世界坐标系。
图像坐标系即为摄像机采集到的图像中的坐标系。其形式为标准电视信号形式，并以M × N的数组输入计算机，数组中的每一个值（或三个）即为该像素的亮度（或RGB值），而它所对应的X和Y的值即为该像素的横、纵坐标。所有的像素点构成了图像坐标系，如图8.2所示。
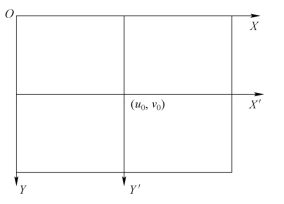
图8.2 图像坐标系
图8.2中的图像坐标系的原点在图像的左上角，单位为像素。此坐标的含义只代表了该像素点在数组中的位置，因此为了方便与相机坐标系的转换，一般会转换坐标系，将坐标原点设在像平面与光轴的交点（u0，v0）（一般为图像中点），即将XOY坐标系转换为X′OY′′图像物理坐标系，见图8.2，并将像素坐标转换为物理长度（如mm）为单位的图像物理坐标。X′O′Y′的原点位于（x0，y0），坐标轴为与原X轴、Y轴平行的X′轴和Y′轴。如果设（u，v）为原图像坐标系XOY中某点坐标，（x，y）为新的坐标系X′OY′′中对应点的坐标，那么它们将有如下的转换关系：
式中，dX、dY为新的图像物理坐标系的物理单位与图像坐标系的像素单位的转换关系。该转换关系可用齐次坐标和矩阵形式转换为
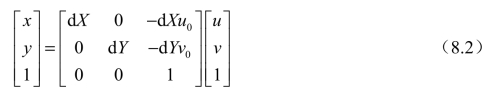
逆转换为
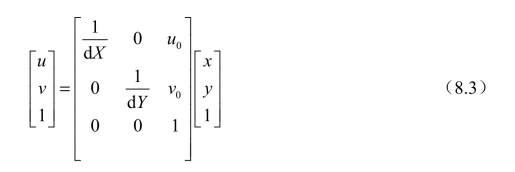
相机坐标系是以相机的光心O为原点，ZC轴与光轴重合，XC轴和CY轴分别与图像物理坐标系的坐标轴X′轴和Y′轴重合。光轴与像平面的交点1O点为图像物理坐标系的原点。OO1的长度即为相机的焦距。
世界坐标系的原点建立在大地上的某点，XW轴和YW轴所构成的平面XWOYW 为水平面，ZW轴竖直向下。世界坐标系和相机坐标系的关系可以通过坐标系的平移和旋转来描述，因此可以构造出二者间的平移向量T和旋转矩阵R。设空间中某一点P在世界坐标系下的齐次坐标为（XW，YW，ZW ，1），其在相机坐标系下的坐标为（XC，YC，ZC ，1），二者的转换关系可以表示为
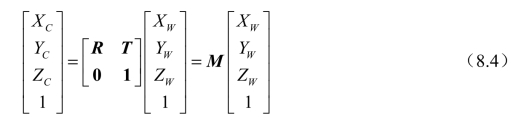
式中，R为3 × 3的旋转矩阵；T为3 × 1的平移向量，即在相机坐标系下世界坐标系的原点坐标；M为4 × 4的转换矩阵。这个矩阵，也正是位置姿态估计所需要求的。如图8.3所示。
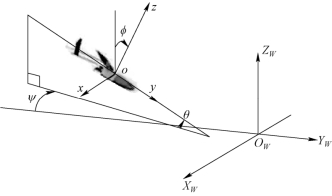
这里默认无人机坐标系oxyz的原点o与相机坐标系的原点是重合的。首先用三个欧拉角来描述无人机相对于世界坐标系的姿态，即俯仰角θ、偏航角ψ、滚转角φ（图8.4）。其中，俯仰角为无人机机体轴oy与世界坐标系XWOYW 平面的夹角，偏航角为无人机机体轴oy与YWOZW 平面的夹角，滚转角为无人机机体轴oz与过无人机oz轴的竖直平面的夹角。
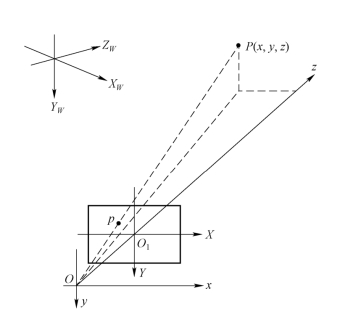
图8.3 相机坐标系与世界坐标系
图8.4 三个欧拉角
除此之外，无人机上所载的云台相机视轴也相对无人机主轴有着旋转变化。也就是说，相机坐标系的旋转矩阵R可以如下表示。
式中，UR为无人机坐标系相对于世界坐标系的旋转矩阵；CR为相机坐标系相对于无人机坐标系的旋转矩阵。相机坐标系相对于无人机坐标系的欧拉角为俯仰角Cθ和偏航角Cψ。
因此，世界坐标系和相机坐标系之间的转换关系可以表示为
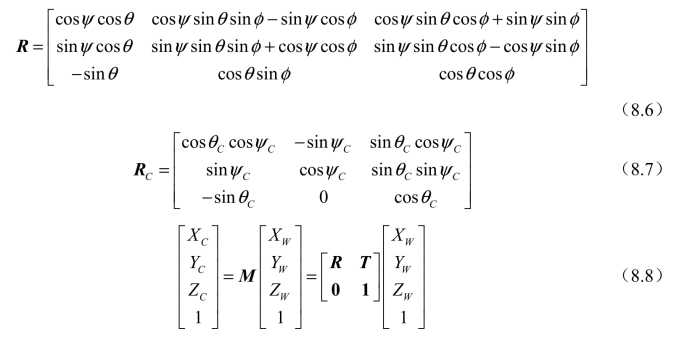
而相机坐标系和图像坐标系之间还有一个转换关系，这是一个将三维齐次坐标变换为二维齐次坐标的变换。如图8.5所示。
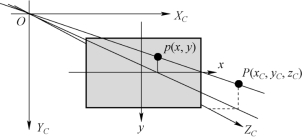
图8.5 相机坐标系与图像坐标系
这里P（xC，yC，zC）是实际存在的某个点，p（x，y）是P点所对应的像素点。理想情况下，像平面是垂直于光轴的平面，因此点p在相机坐标系中的坐标为（x，y，f）。如果不考虑相机畸变，P点与p点会在一条过相机坐标系原点的直线上，会有如下的比例关系成立：
从而
可以用矩阵形式表示为
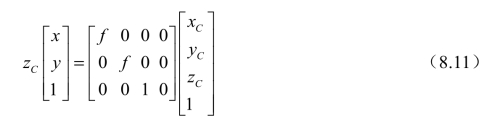
结合式（8.3）、式（8.8），式（8.11）可化为
