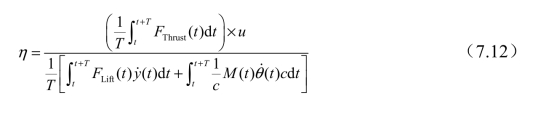7.2 MAV系统模型
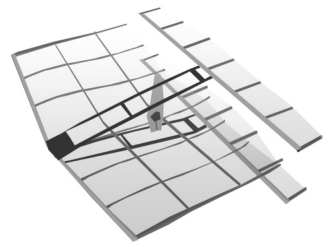
图7.1 微型扑翼飞行器
本章试验主要以NPS提出的微型扑翼系统模型为基础，详见图7.1。NPS flapping-wing MAV（微型扑翼飞行器）是美国海军研究生院设计的一种扑翼推进装置，此款样机由一个前端固定翼和后方的一对拍动尾翼组成。固定翼提供升力，而推力由扑翼来提供，扑动频率约为20 Hz。由于这种固定翼主要提供升力而扑翼主要提供推力的结构，研究者能更好地研究扑翼提供的推力和推力效率，进而便于研究微型扑翼系统的气动特性。
接下来从该模型中，将三维的微型扑翼系统简化到二维研究，如图7.2所示。此时，可以忽略扑翼系统在飞行器水平飞行过程中翼的水平方向位移，因此位移相对很小，忽略并不会对计算结果产生较大影响。此时微型扑翼飞行器的扑翼运动可以简化成如下两个周期方程：
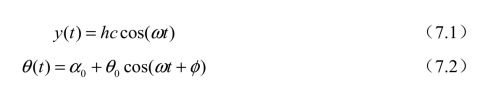
式中，y（t） 为沉浮运动（plunging motion）；θ（t）为俯仰运动（pitching motion）；h为沉浮运动的无量纲幅值；c为弦长；hc为沉浮运动幅值；ω为单位为弧度/秒的角速度，角速度有时候也用2πf来表示，其中f为扑动频率；0α为运动初始攻角；0θ为俯仰运动的幅值；φ为俯仰运动和沉浮运动之间的相位超前角。图7.2中O点是俯仰运动的旋转支点，a是从翼前端到旋转支点的无量纲长度。对于纯沉浮运动，有α0=0.0、θ0=0.0和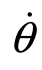
（t）=0.0。
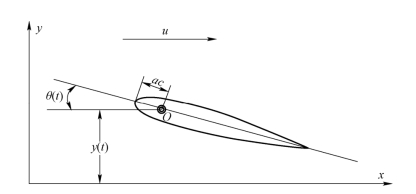
图7.2 扑翼的数学模型
此外，雷诺数（Re）和斯特劳哈尔数（Sr）由以下公式计算。前者用来表示流体的黏性，后者表示扑翼速度和远方来流速度的相似度。这两个参数的计算公式分别如式（7.3）和式（7.4）所示。
式中，ν为流体的运动学黏度；A为扑翼的尾迹宽度，可以直接简化为沉浮运动振动幅值的2倍。
由经典的空气动力学理论可知，阻力系数Cd、升力系数Cl和俯仰力矩系数Cm的定义如下：
式中，xF和yF为气动力的合力沿水平方向和竖直方向的分量；ρ为流体密度；S为扑翼面积。对于二维问题，很难界定参考面积，于是在本章此后的论述里使用推力（thrust）和升力（lift）来讨论MAV（微型飞行器）的气动特性。俯仰力矩的参考点即为俯仰运动的旋转支点，俯仰运动的讨论中旋转支点定位扑翼前缘，即a=0。L是参考长度且与弦长相等。设计者往往更关心微型扑翼飞行器在一个周期内的推力和升力变化，以及推进效率。推力/升力随时间变化曲线均在稳定后取一个周期来研究。至于推进效率η由式（7.8）定义：
式中，u为来流速度；
为一个周期的平均推力系数；
为驱动机翼扑动的功系数。
、
分别由式（7.9）和式（7.10）计算：
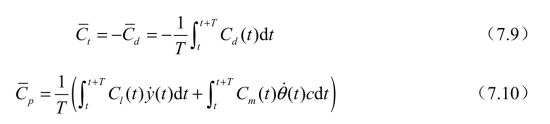
式中，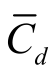
为一个周期的平均阻力系数；
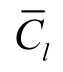为一个周期的平均升力系数；
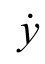（t）和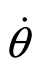
（t）分别为y（t）和θ（t）的一阶时间导数。由于扑翼相当于只提供推力，升力在一个周期内平均值为0，因此推力作用就是扑翼驱动作用的体现；又由于实验中用到的是力而不是升力/推力系数，本章中用力代替力系数进行计算。将上述式子代入式（7.8）再简化：
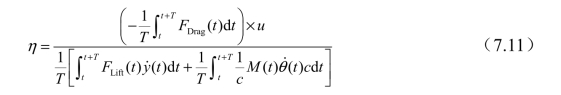
将阻力换成推力可得
