习题3
3.1 欧拉运动微分方程和伯努利方程的前提条件是什么，其中每一项代表什么意义？
3.2 设进入汽化器的空气体积流量为Q=0.15m3/s，进气管最狭窄断面直径D =40 mm，喷油嘴直径d=10 mm。试确定汽化器的真空度。又若喷油嘴内径d=6 mm，汽油液面距喷油嘴高度为50 cm，试计算喷油量。汽油的重度γ=7355N/m3。
3.3 已知欧拉参数表示的速度场分布为u=x+t，v=y+t，试求质点位移和速度的拉格朗日表达式。已知t=0时x=a，y=b。
3.4 绘出下列流函数所表示的流动图形（标明流动方向），计算其速度、加速度，并求势函数，绘出等势线。（1）ψ=x+y；（2）ψ=xy；（3）ψ=xy；（4）ψ=x2+y2。
3.5 已知平面不可压缩流体的速度分布为：（1）u=y，v=-x；（2）u=x-y，v=x+y；（3）u=x2-y2+x，v=-（2xy+y）。判断是否存在势函数φ和流函数ψ，若存在，则求之。
3.6 已知欧拉参数表示的速度分布为u=Ax，v=-Ay，求流体质点的轨迹。
3.7 已知流场的速度分布为u=x+t，v=-y+t，求t=0时通过（-1， 1， 1）点的流线。
3.8 请以螺旋桨为例，叙述用Fluent计算滑移网格的设置过程。
3.9 已知平面不可压缩流体的速度分布为2 u=xt，v=-2xyt，求t=1时过（-2， 1）点的流线及此时处在这一空间点上流体质点的加速度和轨迹。
3.10 设不可压缩流体的速度分布为：（1）u=ax2+by2+cz2，v=-dxy-eyz-fzx；（2）u=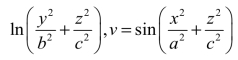
。其中a、b、c、d、e、f为常数，试求第三个速度分布w。
3.11 有一扩大渠道，已知两壁面交角为1弧度，在两壁面相交处有一小缝，通过此缝隙流出的体积流量为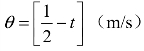
，试求：（1）速度分布；（2）t=0时壁面上r=2处的速度和加速度。
3.12 已知不可压缩平面势流的分速度为u=3ax2-3ay2，（0，0）点上u=v=0，试求通过（0，0）及（0，1）两点连线的体积流量。
3.13 设流场的速度分布为u=ax，v=ay，w=-2az，其中a为常数。（1）求线变形速率、角变形速率、体积膨胀率；（2）问该流场是否为无旋场？若是无旋场求出速度势。
3.14 设流场的速度分布为u=y+2z，v=z+2x，w=x+2y。试求：（1）涡量及涡线方程；（2）x+y+z=1平面上通过横截面积dA=1mm2的涡通量。