9.3.2 无人机的变速追踪着陆过程
若车辆在路面上保持匀速行驶,无人机的自主着陆过程可以理想近似于导弹平行接近法制导的过程,这是理想情况,但是现实中车辆可能会有减速或者加速的情况,这种情况就需要无人机针对车辆的速度变化改变角σ的值,即改变运动路径。
当车辆加速的时候,需要相应减少σ的值,令无人机的飞行轨迹向上偏移,将无人机的着陆位置向后移动一段距离,使无人机能够继续保持视线角一定执行追踪着陆过程,车辆加速过程中的追踪着陆过程如图9.4所示。
因为在自主着陆过程中,可以通过降低无人机速度矢量竖直方向的分量vUY,使速度方向角σ的值减小。当视线角q的值重新回到标准值45°时,通过对水平距离l求积分得到Cv,用式(9.20)求得新的无人机速度矢量水平分量vUX,之后重新进行着陆过程。
而对于车辆减速的情况,则需要增大无人机速度方向角σ,使无人机的飞行轨迹向下偏移,这种情况下预计着陆位置会向前移动,使无人机能成功接近车顶。车辆减速过程的追踪着陆过程如图9.5所示。
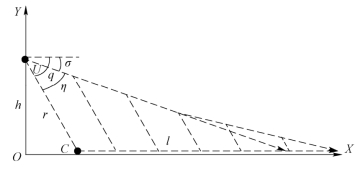
图9.4 车辆加速过程中的追踪着陆过程
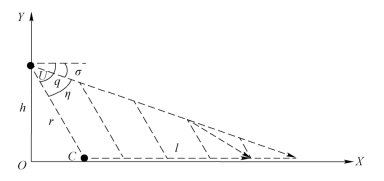
图9.5 车辆减速过程的追踪着陆过程
在这种情况下,需要降低无人机速度的水平分量vUX,使无人机速度方向角σ增大。这时为了保证无人机在竖直方向上的稳定,控制停止无人机的下降,令其悬停在当前高度,当视线角重新回到标准值时,重新通过新的Cv计算vUX并重新开始着陆。
因为在无人机自主着陆的过程中,在发生加减速前车辆对于无人机的视线方向角q是不变的,即车辆上的用于视觉识别的标志物的中心点在无人机机载云台相机所拍摄的图像中位置是不变的。因此可以简单地判断出车辆的加减速,从而进行调整。下面将介绍具体的调整方法。
本章之前提出了四旋翼无人机的数学模型和动力模型[式(9.1)~式(9.13)]的部分内容。
在四旋翼无人机自主着陆过程中,滚转角φ和偏航角ψ,以及机体坐标系下的滚转角速度p和偏航角速度r可以看作0。因此,不考虑Y方向,上述模型的部分方程可以简化为
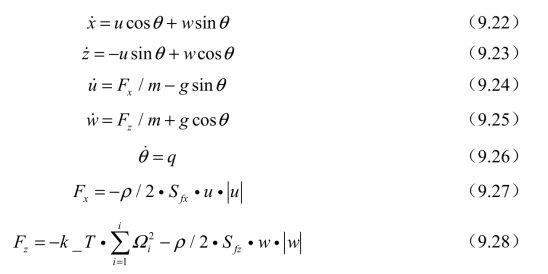
排除四旋翼无人机飞行过程中空气阻力对无人机的影响,动力学模型可以简化为

对X、Z方向的速度进行微分,得到
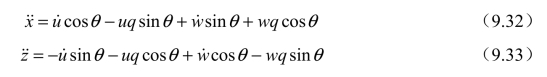
M100的绕俯仰轴最大转速为300/s°,最大俯仰角为θ=35°,因此俯仰运动是在很短的时间内完成的,可以假定这个过程是瞬时的。此时,式(9.32)和式(9.33)可以写为
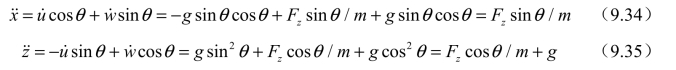
视线方向角q可以表示为

式中,z为无人机所处的相对高度;l=x-xc 为开始着陆时无人机与车辆间的水平距离,xc为车辆所行驶的距离,并且有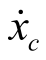 =vc。
=vc。
无人机的速度方向角σ可以表示为

在车辆减速的过程中,cv随时间t变慢,令z保持一定的高度,若使p保持不变,则需要使l保持与减速之前相等,即Δl=0。
因为要令无人机保持一定的高度,所以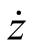 =0,
=0,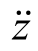 =0,即 (https://www.daowen.com)
=0,即 (https://www.daowen.com)
![]()
可以根据等式(9.38),将其代入式(9.34),得到
![]()
因此,车辆减速过程中,四旋翼无人机的数学模型可以总结为

当通过无人机对于标志物的图像识别发现视线方向角q增大一定值时,停止降落运动,令z保持一定的高度,同时通过对l进行求导可以得到此时车辆变速后的速度cv。
对视线角q及水平方向距离l进行闭环控制,如图9.6所示。
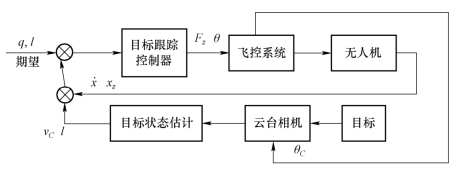
图9.6 变速过程中无人机跟踪系统框图
对这一过程用Matlab中的simulink设计PID(比例-积分-微分)反馈回路,回路的构造如图9.7所示。
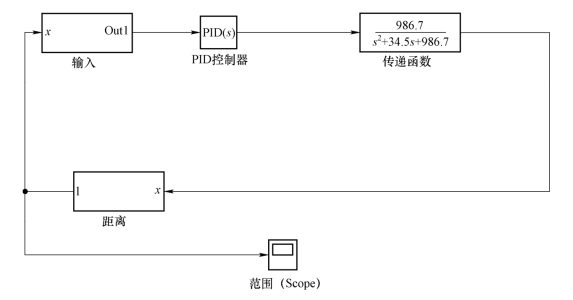
图9.7 减速过程PID反馈回路
其中,系统的传递函数为

在对PID控制器进行调参之后,得到无人机与车辆的水平距离的控制曲线以及视线角的控制曲线,如图9.8所示。
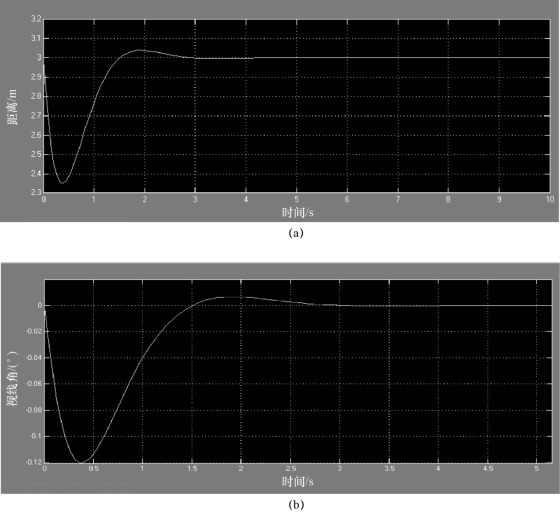
图9.8 水平距离的控制曲线以及视线角的控制曲线
(a)水平距离的控制曲线;(b)视线角的控制曲线
当车辆加速时,无须提高vUX的值,只要降低无人机速度向量的竖直分量vUY,即可令视线角q保持一定。
无论车辆加速或者减速,在保持视线角q为定值之后,再根据车辆的车速vC对无人机的速度方向角σ和无人机速度向量的水平分量vUX进行解算,之后再次开始追踪降落。
若此时vUX上升到无人机所能允许的最大值,则若要使视线角q恒定,则需要减少无人机速度向量的竖直分量vUY,即 。在改变
。在改变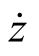 时,无人机的速度向量水平分量保持不变,则俯仰角θ=0,那么有式(9.42)成立:
时,无人机的速度向量水平分量保持不变,则俯仰角θ=0,那么有式(9.42)成立:
![]()
维持视线角q的闭环控制如图9.9所示。
若车辆速度继续增加,导致无人机的速度向量的竖直分量减少到0,此时无人机着陆已不可能。这时车辆的临界速度vC=vUX =17m/s,即61.2 km/h。超越了这个车速着陆是不可能的。
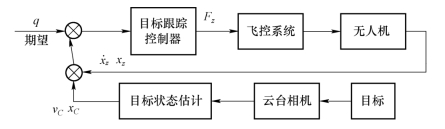
图9.9 加速过程以及极限加速过程的无人机跟踪系统框图
