8.3.2 Tsai的RAC两步标定法
Roger Y.Tsai在1987年提出了一种基于径向约束的两步标定法，它的具体解法如下所示。
由世界坐标系到相机坐标系的方程可以写为
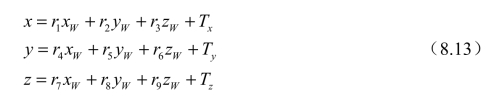
由于镜头的径向畸变，像点的坐标会有一定的径向偏离，可以假定，偏移前的像点的像素物理坐标为（x0，y0），偏移后的像坐标为（x0+Δx，y0+Δy），那么，它们将不再符合投影关系，但是即便如此，它们还是会符合如下的比例关系：
此为RAC（径向准直约束），将式（8.13）代入可得
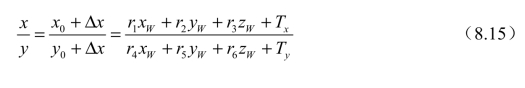
整理可得
令Xd =x0+Δx，Yd=y0+Δy，可以将式（8.16）展开整理为
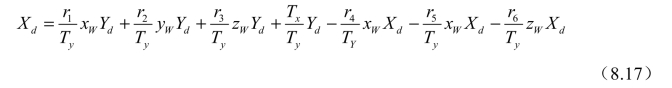
化为矢量式为
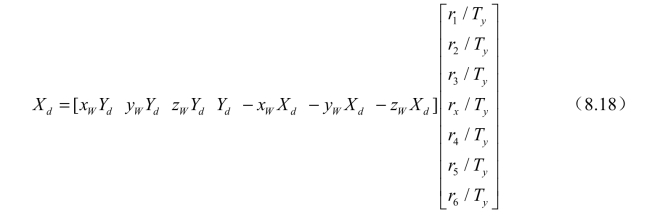
其中，
是已知的，而矢量
是未知矢量，也就是待求的参数。根据式（8.3），可以将图像物理坐标（Xd，Yd）转换为图像像素坐标（ud，vd）：
式中，sx为横纵比。设有n个共面点（xWi，yWi，zWi），它们对应的图像像素坐标为（udi，vdi），i=1，2，3，…，n，令所有的zWi =0，之后标定过程如下。
（1）解旋转矩阵R，平移向量的tx，ty分量。
通过式（8.19）对（udi，vdi）求解其所对应的（Xdi，Ydi）。
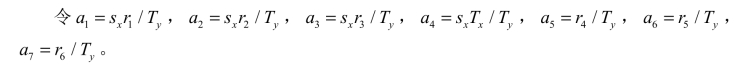
由于
根据正交性，即
，则有
之后从标定点中选一个点，并假定Ty＞0，进行如下计算：
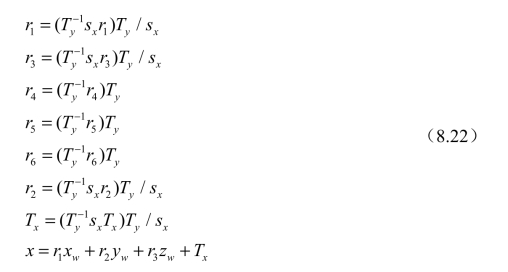
若Xd与x同号，dY与y同号，则yT符号为正，否则为负。根据旋转矩阵R的正交性，计算7r、8r、9r如下：
（2）求解zT、f和畸变系数k。
根据不考虑畸变情况的相似关系，有
令k=0，根据式（8.13）和式（8.15）可得
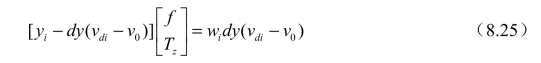
其中，yi=r4xwi+r5ywi+r6zwi+Ty，wi=r7xwi+r8ywi+r9zwi，求解式（8.25）的超定方程组，可得f和Tz的初始值。
令初始值k=0，（u0，v0）的初始值为屏幕中点，通过对下列方程的求解以及优化搜索可得到f、k、Tz、（u0，v0）的精确解：
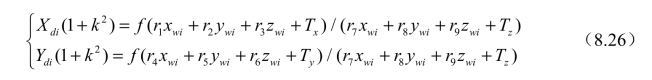
之后根据第一步中解得的R以及云台相机的姿态角进一步解算出无人机的三个欧拉角。