4.3.2　流线追踪

欧拉法认为流场的每一点都有速度。在流场中每一点上都与该点在流场内的速度矢量相切的曲线称为流线。对于定常流动来说，流线的形状是不随时间变化的。可以认为，若在流线上放一个质点，则流线即是质点的运动轨迹。流线上的每一点的切线在3个方向的余弦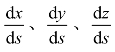和流速的3个方向分量vx、vy、vz与合速度V所夹的3个角度的余弦相同，表示成微分形式的关系为

由锥形激波流场与特征长度无关且具有对称性可将三维流场简化为二维流场，这时流场中dz=0，则转化后流场的流线方程为

为方便计算，现将式（4.11）转化至球坐标系下。直角坐标系与球坐标系之间的转换关系为

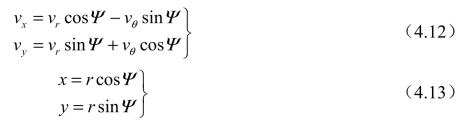
从而可以得到球坐标系下的流线方程为

vr，vθ可以通过Taylor-Maccoll方程求解得到的流场数据中得到。之后将式（4.14）通过四阶Runge-Kutta法求解得到流线。