4.4.2 频域分析
频域分析是将脑电信号变换到频域,从频域提取脑电信号相关特征,直接观察δ、θ、α、β、γ节律的分布与变化。功率谱估计是频域分析的一种重要方法。但谱估计分析脑电信号的平均谱特征,会丢失脑电的瞬态信息,一般无法检测到癫痫中的棘波和尖波。谱估计法大致可以分为非参数模型谱估计与参数模型谱估计,非参数模型谱估计又称为经典谱估计,主要有自相关法、周期图(periodogram)法、Welch法等;参数模型谱估计主要有自回归(AR)模型谱估计、滑动平均(MA)模型谱估计、自回归滑动平均(ARMA)模型谱估计等。
1.傅里叶变换
法国数学家约瑟夫·傅里叶(1768—1830)在研究偏微分方程的边值问题时提出了傅里叶级数(Fourier series,FS)的概念,傅里叶级数可以将任何周期函数或周期信号分解成一组简单振荡函数的和,即可以用正弦函数和余弦函数表示。然而,并非所有的信号都是周期信号,所以对傅里叶级数的概念进行了延伸,即将函数的周期延长并被允许接近于无穷大时可以导出傅里叶变换。当一个函数满足狄利克雷条件即在无穷区间内绝对可积时,则傅里叶变换式(4.1)成立:

式中,w代表角频率。f(t)为原函数,F(w)称为f(t)的像函数,二者共同组成了一对傅里叶变换对。在计算机信号分析中,采用离散傅里叶变换(discrete Fourier transform,DFT),通过对离散时间傅里叶变换(discrete-time Fourier transform,DTFT)频域上的采样,使得傅里叶变换在时域和频域上都呈现离散的形式,离散时间序列x(1),x(2),x(3),…,x(n)的傅里叶变换为

2.功率谱密度
上述傅里叶变换的基本原理均为以下经典谱估计分析方法的基础。功率谱密度(power spectral density,PSD)根据随机信号x(n)和自相关函数r(k)计算,公式为
![]()
其中,r(k)=E[x(n)x*(n+k)],E代表数学期望,*代表复共轭。
3.周期图法
假设脑电是平稳信号,将脑电信号进行准平稳分段,使信号序列为有限长度,可以得到周期图谱估计:
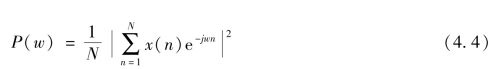
周期图法中,分辨率随着数据长度增长而增加,但方差不会减小。
4.加窗周期图法
为改变周期图法谱估计性能,减小方差,可以采用与适当谱窗卷积来平滑周期图,即
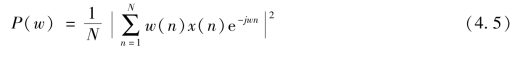
式中,w(n)代表窗函数,常用的窗函数有矩形窗、三角窗、汉宁窗、哈宁窗和布莱克曼窗,矩形窗频率分辨率最高,但其旁瓣也最高。(https://www.daowen.com)
5.平均周期图法
平均周期图法也能达到减小方差的目的。将总长为N的数据分为M段,每段长度为L,分别计算每一段的周期图,然后进行平均:
![]()
平均周期图法频率较周期图法方差减小M倍,但频率分辨率下降了M倍。
6.W elch法
Welch法以加窗进行平滑,以分段重叠求取平均,因此集平滑与平均的优点于一体,但也不可避免地存在缺点。实际应用中由于易于理解,便于计算,多数情况下频率分辨率和方差性能可以满足需要,因此Welch法被广泛应用。
该方法将数据分段加窗后求傅里叶变换,分段的数据允许重叠,每个分段数据采用加窗运算。将总长为N的数据分为K段(可重叠),每段长度为L:
![]()
其中,V表示窗函数w(n)的功率,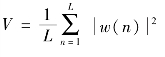
7.自回归模型谱估计
经典谱估计存在分辨率低、方差性能差的问题,根本原因在于谱估计时需要对数据进行加窗截断,采用有限个数据或其自相关函数来估计无限个数据的功率谱,意味着在窗外的数据全部置为0,但是这种假设并不符合实际。而现代谱估计主要是针对经典谱估计(自相关法、周期图法等)的问题进行改进。MA模型需要求解非线性方程组进行参数估计,而ARMA模型则需要确定AR与MA的阶数再进行参数估计,过程较为复杂烦琐,因此AR模型计算相对简单并且在高信噪比的条件下频率分辨率高,因而更加常用。但AR模型谱估计在信号为线性、平稳性的条件下估计性能较好,而脑电信号是非平稳信号,因此进行AR模型谱估计时一般将脑电信号分段。AR模型谱估计法假设所研究的信号x(n)是一个输入序列u(n)激励一个线性系统H(z)的输出,然后使用已知的x(n)对模型的参数进行估计,再从H(z)的参数估计x(n)的功率谱。
AR模型是一个全极点模型,即
![]()
p阶AR模型的参数为ai(i=1,2,…,p),u(n)为白噪声序列,对其进行Z变换,则AR模型的传递函数为
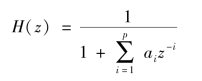
则x(n)的功率谱密度为
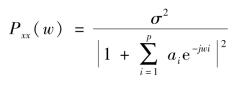
其中,σ2为白噪声序列方差,一般可以采用自相关法、Burg算法、改进协方差算法等进行AR模型参数求解,此处不再对具体算法展开叙述。与经典谱估计方法相比,AR模型谱估计法可以得到连续频率的频谱,模型阶数越高,分辨率越好,但阶数过高会导致存在伪峰值,因此可以使用最终预报误差(final prediction error,FPE)准则法、赤池信息准则(Akaike information criterion,AIC)等方法确定AR模型的阶数。
