4.5.3 复杂脑网络分析
网络是现实世界中复杂系统的数学描述,定义为一组节点和双节点之间的连接,反映线性或非线性的相互作用,以及在不同的时间尺度上的相互作用。大脑是自然界中一个极其复杂的网络,其复杂性不仅体现在大量神经元以及这些神经元之间数以万亿计的连接,而且体现在这些连接模式产生的行为和认知功能等。研究复杂脑网络的技术手段多种多样,采用脑电图研究复杂脑网络,具有方便、无创、经济效益高、获取容易、可实时监控、时间分辨率高(毫秒级)等优势,并且能够为实验研究提供神经元在时域、频域、脑区分布的多种特征参数,大量应用于静息态和任务态的脑电信号分析。
目前在复杂网络分析中主要采用基于图论的方法,将人脑看成网络,采用二元连接矩阵和连接之间特定的生理数据结合来描述大脑拓扑结构。一个复杂网络G(V,E)可以用一个由节点(V)和边(E)的集合构成的图表示,如图4.12所示,空心圆圈代表网络节点,节点之间的连接线代表边。基于脑电信号的脑网络分析主要包括以下步骤:①首先选择合适的网络节点,将头皮电极作为构建脑网络节点;②定义连接边,选择度量指标来表征节点之间的关联强度,得到大脑的连接矩阵。通常情况下,通过度量不同节点的时间序列之间的相关性来建立连接边,即衡量两个电极之间信号的相位同步性,常用方法包括互相关(cross-correlation)、互信息(mutual information,MI)、同步似然(synchronization likelihood,SL)、相位滞后指数(phase lag index,PLI)等。除了无向功能连接分析方法,有向功能连接显示不同区域或电极之间信息的流向和交互作用,主要有格兰杰因果关系(Granger causality,GC)分析、结构方程模型(structural equationmodeling,SEM)分析以及动态因果模型(dynamic causalmodelling,DCM)分析等;③选择合适阈值以确定节点之间是否存在连接边的关联。节点之间的关联关系可以用二值矩阵描述,如果任意节点i、j间存在边则二值矩阵此元素aij值为1,相反则为0。
1.相位滞后指数
相位同步性是大脑功能整合的一种机制,相位滞后指数是检查一对信号之间相位差分布不对称性的一种度量,反映了特定频率下两两电极之间跨试次相位变异的程度。同时通过相位滞后指数可以有效避免容积导体效应。引入PLI的主要目的是计算相位差的分布规律,获得可靠的相位同步估计,这些分布表现为与0的差值。任何偏离该分布的偏差都表示为相位同步性。相位差分布的不对称性意味着,相位差在间隔-π<φ<0的可能性与在间隔0<φ<π的可能性是不同的。这种不对称性表明,在这两个时间序列之间存在持续、非零的相位差(相位滞后)。相位差分布的不对称性指数由以下方式,通过计算相位差的时间序列获得
![]()
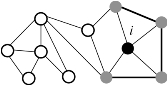
图4.12 网络G(V,E)(https://www.daowen.com)
PLI在0~1范围内变化。如PLI值为0,表示两个信号不存在耦合关系,或与以接近于0 modπ为中心的相位差存在耦合关系。如PLI值为1,则表示两个信号有完美相位锁定且φ值与0或π不同。这种非零相位锁定越大,PLI值越大即越接近于1。
2.动态因果模型
相位同步性属于同步性分析方法,如果两个电极或者脑区信号具有同步性,那么就说明两个电极或者脑区之间存在相互联系,但是无法给出二者是如何相互影响的。如果可以建立神经元之间相互作用的因果关系,反映神经活动的动态过程以及实验对神经活动的调节,则可以更加接近真实的脑功能机制。动态因果模型方法可以建立有效的有向连接,其将大脑看作一个确定的非线性动力学系统,通过在神经元状态空间建立模型估计大脑不同脑区之间的信息整合和流动情况,将大脑表示成一个动态的“输入-状态输出”系统。对于脑电信号,DCM由神经元动力学的生成模型和记录的电信号x*的观测模型构建,生成模型可用状态方程表示:
X=f(x,u,θ)
其中,x代表神经元群的状态变量,u代表模型外部输入,θ则代表模型参数集。此状态方程可以描述在此网络中某个神经元活动映射到另一个神经元活动的演变过程。对于所记录的脑电信号x*,可以用观测方程描述:
x*=L(φ)x0+ε
式中,x0代表表层锥体细胞的去极化跨膜电位,ε是高斯误差。观测模型在脑网络中建立等效电流偶极子源,L(φ)代表电磁场引导矩阵。此方程用以描述观测信号与神经元活动之间的映射关系。
