6.3.3 聚类分析
聚类分析是一种无监督学习方法,是指从没有标签的输入数据中绘制参考。其通常被用于找到有意义的结构、可解释的潜在过程、生成特征和一组样本中的固有分组。聚类完成的任务是将人或数据点分成一些小组,使得同一组中的数据点和同组内的数据点更加相似,而和其他组的数据点不相似。其通常基于数据点之间的相似性和不相似性进行分组。图6.13中聚类到一起的数据点可以被分入同一组。我们可以区分出这些类别,并且观察到有三种类别。
聚类非常重要的一点是用于确定现有未标签数据的固有分组。聚类没有统一的标准,取决于使用者,标准即使用满足需求的聚类。因此,我们可能对以下几方面感兴趣,即找到同质的组的表示(数据压缩),找到“天然的聚类”(natural clusters)并且描述其未知属性(天然的数据类别),找到有用的和适合的分组(有用的数据类别),找到不寻常的数据目标(异常值检测)。
1.聚类方法
(1)基于密度的方法。这类方法认为聚类是有相似性的密集区,有别于空间中的低密度区,具有很高的准确性和能力去合并两个聚类。例如,基于密度的噪声应用空间聚类(density-based spatial clustering of applications with noise,DBSCAN),点排序以识别聚类结构(ordering points to identify the clustering structure,OPTICS)。
(2)基于分层的方法。这种方法的聚类形成一个基于层级的树形结构,在前一个基础上形成新的聚类,被分成会凝聚的(自下而上的方法)和分裂的(自上而下的方法)两类。例如使用表示进行聚类(clustering using representatives,CURE),平衡迭代减少聚类和使用层级结构(balanced iterative reducing clustering and using hierarchies,BIRCH)。
(3)分割方法。这类方法将目标对象分割成K个聚类,每个分区形成一个聚类。用于优化目标准则相似函数,如K均值和CLARANS(clustering large applications based upon randomized search,基于随机搜索聚类大型应用程序)中距离是一个主要的参数。
(4)基于网格的方法。在这个方法中数据空间被配制成有限数量的单元,形成一个网状结构。所有网格上的聚类操作独立于样本数量,例如STING(统计信息网格,statistical information grid)、小波聚类、CLIQUE(任务中的聚类、clustering in quest)等。
2.聚类算法
K均值聚类算法:是最简单的解决聚类难题的无监督学习算法。K均值聚类算法将n个观察值分成K个聚类,其中每个观察值属于具有最近均值的聚类。
K均值聚类算法的输入是类别数量K和数据集。数据集是每个数据点的特征集。首先估计出原始的K个聚类中心,这些聚类中心可以是随机生成的或者从数据集中随机挑选的。然后算法会在两个步骤之间迭代。
第一步,数据分配。每个聚类中心定义其中的一个类别。这一步中,通过计算欧几里得距离的平方,每个数据点被分配给离它最近的聚类中心。即如果ci是集合C中的聚类中心之一,那么每个数据点x用以下公式分配给某个类别:(https://www.daowen.com)
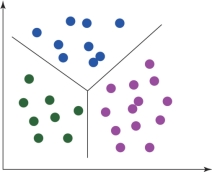
图6.13 聚类(书后附彩插)
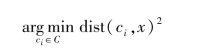
其中,dist(·)为标准的欧几里得距离的L2范数。我们将分配到第i个聚类中心的数据点集合定义为Si。
第二步,聚类中心更新。这一步中聚类中心被重新计算,即将Si内所有数据点求均值,作为新的聚类中心。
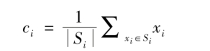
K均值聚类算法在步骤一和步骤二之间迭代,直到满足终止条件(如没有数据点改变聚类结果,距离之和最小,或是达到了最大迭代数目)。这个算法会确保收敛到一个结果,结果可能是一个局部最小值(即不一定是最好的结果),这意味着在使用该算法时,随机选择初始聚类中心并多运行几次,可能会得到更好的结果。
以上提到的算法都是在一个预定的K值上找到类别并为数据贴上标签。为了找到数据中类别的数量,我们需要在一定范围的K值中运行K均值聚类算法并且比较结果。通常来说,我们没有办法确定K的真值,但是可以使用以下方法获得准确的估计。
一种方法是比较不同K值下数据点和它们聚类中心之间的平均距离。既然随着聚类数目的增加,聚类中心和数据点之间的距离总是会缩短,那么K值增大时就总是会使平均距离变小,当K和数据点数目一致时,平均距离为0。那么数据点和聚类中心的平均距离是K的函数,函数拐点(elbow point)是下降率急剧改变的点,可被粗略用于确定K的取值。
其他用于确定K值的方法包括交叉验证、信息准则、信息理论跳跃、轮廓方法和G均值算法。并且,检查不同组数据点的分布可以深入了解算法是如何分割每个K的数据的。
聚类可以应用于很多领域。例如,市场营销中用于归纳和发现顾客片段,生物学中用于不同动植物种类的分类,图书馆中基于话题和信息将不同的书籍聚类,保险中用于确认顾客的保单和识别诈骗,城市规划中基于地理位置和其他现有因素研究不同组的房屋价值,地震研究中用于通过学习受地震影响的区域决定危险区域。
