6.2.2 图论分析
在图论中,一个复杂网络G(V,E)可以用一个由节点(V)和边(E)的集合构成的图表示。其构建过程主要包括三个步骤:①首先选择合适的网络节点;②定义连接边,选择度量指标来表征节点之间的关联强度,得到大脑的连接矩阵;③选择合适阈值以确定节点之间是否存在连接边的关联。节点之间的关联关系可以用二值矩阵描述,如果任意节点i、j间存在边则二值矩阵此元素aij值为1,反之则为0。
基于边的网络矩阵(通常也叫作“图”),使用图论技术能够进行进一步的基于节点的分析。图论分析并不是直接在组间比较网络矩阵,而是使用该矩阵提取更高水平的用以描述网络功能的概括性指标。代表性地,图论分析使用相关计算网络矩阵的边,随后将网络矩阵阈值化成为一个二值矩阵(意味着边为1或0,也就是两个节点之间要么有边,要么没边)。二值化后,通常会有10%~20%数量的最强的连接边被保留下来。这个二值化(也叫作无权)网络矩阵可用于提取网络特征的局部和全局指标。最常见的图论指标如图6.6所示。
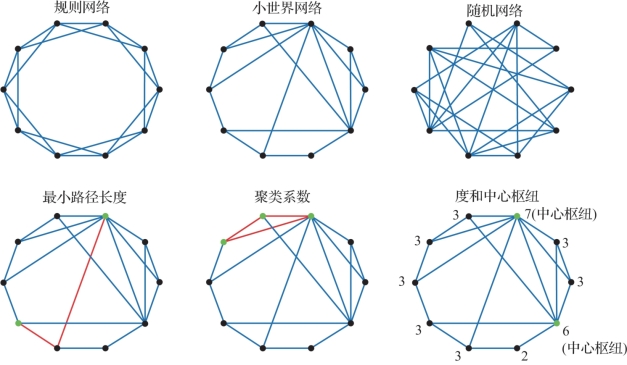
图6.6 计算网络功能的指标(摘自Bijsterbosch,J.,et al.2017[3])(书后附彩插)
节点指标:两个节点之间的最小路径长度定义为从节点A到节点B所必需的最小边的数目。一个节点的聚类系数测量的是与该节点相连的节点之间存在连接的数目。因此,一个高的聚类系数意味着,如果节点A和节点B都和节点C相连,它们也有可能彼此相连。计算聚类系数需要考虑三角形连接的节点的数量。一个节点的度定义为与其相连的其他节点的数目。如果节点的度高于整幅图的平均节点度,那么该节点称为中心。hub节点通常会和其他hub节点紧密相连(通常通过长距离连接),形成节点的富人俱乐部。
节点度:节点度用以描述节点之间相互连接的统计特性,即与该节点相连的其他节点的数目。对于某一节点i,度D的定义可以采用以下公式来描述:
![]()
其中,N为网络中节点总数;aij为二值矩阵中的值,当aij=1时,此i,j节点间存在相连边,当aij=0时,此i,j节点间无连接。节点度越大,表示该节点在网络中越重要。此外,节点的度分布P(k)也是网络的基本拓扑性质,表示在网络中等概率随机选取度值为k的概率。
全局概括性指标:可以对局部指标中的最小路径长度和聚类系数进行平均后,得到整个图的平均路径长度和聚类系数。并且,所有节点的度分布可以提供某一特定度在网络中出现的可能性的相关信息。全局效率和平均最小路径长度成反比(也就是平均路径长度分之一),是整幅图效率的度量。小世界属性是在许多复杂系统中发现的一种网络特性,如社交网络、互联网以及大脑。小世界网络组织意味着节点之间局部存在紧密连接,而在hub节点之间存在一些长距离的连接。在这种方式下使用hub对于描绘网络效率是很有益处的。因此,小世界网络的特点是低的最小路径长度和高的聚类系数。小世界网络属性的计算可以通过和随机网络进行最小路径长度和平均聚类系数的比较得到。
聚类系数:聚类系数是网络节点倾向于聚在一起的程度,反映某一节点i的邻居节点互为邻居的可能性,可以以某一节点为中心临节点之间三角形数量来计算,即
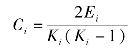
其中,Ei为与节点相连的邻居节点间实际存在的边数;Ki为邻居节点的个数。聚类系数计算为邻居节点之间的连接与所有可能连接的数量之比。
在复杂网络中,如对每个节点都进行聚类系数的计算,数据量较大,因此通常使用全局聚类系数进行评价,即每个节点聚类系数的平均值:(https://www.daowen.com)
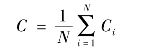
全局聚类系数表征网络节点形成集团的能力。C值越大,网络节点之间的结构越发紧密。当C=1时,网络任意两个节点之间都存在边;当C=0时,任意节点间都没有连接。
特征路径长度:特征路径长度是网络拓扑中最为稳定的三个度量指标之一,用以衡量网络节点间信息交流的潜在途径以及对不同脑区的信息进行快速整合的能力,可以定义为任意两个节点之间最小路径长度的平均值:
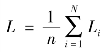
其中,Li为节点i与其他所有节点之间的最小路径长度的平均值。特征路径长度的值反映网络连通性,当特征路径长度越小时,网络的连接强度越大,也即网络结构越紧密,功能整合能力越强。
全局效率:全局效率可以衡量网络全局信息传递及处理的传输能力,定义为最小路径长度的倒数,经此处理可以消除孤立节点的最小路径长度无穷大的问题。其公式如下:
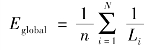
小世界属性:小世界属性是可以表征复杂网络的一个相对简单的统计特性,其确保了人脑利用最小资源选择最优化解决路径以完成任务的能力。同时,网络的“小世界”属性不仅显示了人类大脑的信息交换能力,而且显示了对外界刺激的反应能力与适应能力。小世界网络介于规则网络和随机网络之间,利用特征路径长度与聚类系数来量化网络结构,以随机网络作为标准,定义任意节点间的最小路径长度大致相当于一个随机网络,但具有更大的聚类系数。
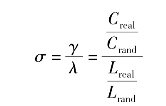
其中,Creal和Crand分别表示真实网络和随机网络的聚类系数;Lreal和Lrand分别表示真实网络与随机网络的特征路径长度。用σ来衡量网络的小世界属性,当σ远大于1时网络具有小世界属性。σ越大,网络的小世界属性越强,信息传输能力及整合能力越强。
一种和度紧密相关的方法是特征向量中心映射(ECM)。ECM实际上是一种基于体素的方法,但是正如我们在这章中提到的,它和前文提到的图论指标有很强的相关性。ECM旨在识别网络结构中发挥核心作用的体素。ECM为每个体素分配一个值,这个值代表它所连接的其他体素的数量,也就是连接的体素的度(即和hub连接得到一个更大的权重)。ECM分析的结果是一个图,代表了每个体素和其他区域相关的强度,表征网络结构的重要性。
这些图论概括性指标可以通过每个被试的数据得到,从而用于组间比较,探索组间(如病人组和健康对照组)网络整合性的差异。常用统计分析方法如t检验可以用于比较概括性指标。因此,图论的优势之一是不必进行多重比较校正(因其分析结果是每个被试一个单独的值,而不是脑图或网络矩阵)。然而,如果将多个图论指标一起比较,需要进行多重比较校正。并且,从图论求得的单个概括性指标可能有助于成为一个简易地反映连接的生物标志物。
虽然将每个被试的复杂网络总结成一个数值很有意义,但这种方法仍然存在劣势。首先,用于图论分析的网络矩阵通常是全相关矩阵,其中包含了节点之间的有向和无向的连接,这对广泛的混合信号(如全脑信号)是很敏感的。其次,将网络矩阵阈值化成为二值图的过程,从没有阈值化的(加权)矩阵中移除了许多潜在重要信息。最后,将二值化边信息减少成为概括性指标,也存在移除有价值信息的风险。因此,图论度量实际上从原始数据中移除了大量信息,因此可能很难解释脑功能图论概括性指标的变化。尽管如此,图论方法仍然能够随着相关问题的改善而变得更有价值,如节点的定义、边估计,以及使用加权(未阈值化)网络矩阵计算的图论指标。
