6.2.1　网络建模

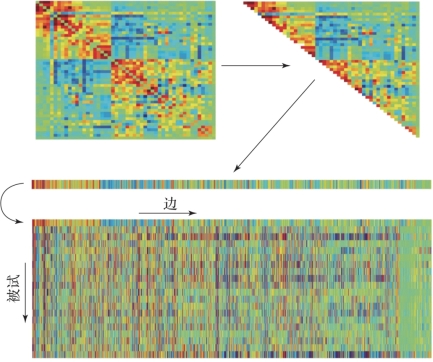
将每个被试的节点乘节点的网络矩阵中所有边都计算完成后，有许多选择可以用于进一步的基于节点的分析。功能网络建模分析保留了网络矩阵中的所有信息，并且在此基础上进行组水平的分析。因此，它使用网络矩阵探索研究问题，例如，哪条边的强度在病人组和健康人组中不同？哪条边在被试间的变化是和感兴趣的行为学变量相关？为了在组水平分析中跨被试比较网络矩阵，被试的网络矩阵有时会被首先结合到一个大的矩阵（被试数乘边数）中。如图6.5所示，通过全相关或偏相关定义边时，会丢弃网络矩阵中的一半（因为矩阵是对称的，如对角镜像），然后从每个被试中集成节点乘节点矩阵中边数的一半，形成一行。多个被试可以堆放在随后的行中，形成一个大的被试乘边的矩阵，该矩阵可以用于组水平分析。

有多种不同的方法可以进行组水平的网络建模分析。第一个是使用大规模单变量方法（mass univariatemethod），该方法分别对每条边进行相同的统计检验。常使用广义线性模型，该方法与基于体素的分析方法相同，比较边，但不比较体素。GLM框架可以进行多种类型数据的比较，包括比较两组或多组、ANOVA和连续变量回归分析。当一个GLM分别应用于每条边时，常常针对要检测的边的数量，对得到的p值进行校正，由此可以控制做大量检验时随机、假阳性结果的发生率（如多重比较校正）。置换检验通常用于对每条边的组间比较。第二个进行组水平网络建模分析的选择是多变量分类（或预测）分析，这种分析可以结合跨越多条边之间的信息，找到最能够区分两组被试的边的模式。分类方法使用一组特征（本例中是边）来找到最能够预测出给定被试属于组1还是组2的模式。最常见的分类方法是线性分类器，如线性判别分析（linear discriminant analysis，LDA），但也有非线性方法。

图6.5　用于组水平分析的矩阵（摘自Bijsterbosch，J.2017［3］）（书后附彩插）

大规模单变量方法的优势在于，每条边的结果仅仅和该条边包含的信息相关，因而解释起来很直观，如GLM。然而，大规模单变量方法对边强度的微小变化不敏感，因为不能在多重比较校正这类相对严格的校正中保留下来。多变量分类分析因为要寻找一种多变量模式，可能对边强度的微小变化（跨越多条边）敏感，在解释分类权重时更具有挑战性，因为结果模式必须被整体解释（虽然分类或预测准确率解释起来更加直接）。

网络建模分析的主要优势是能够进行不同类型的功能连接的研究。特别地，网络建模分析相比于基于体素的方法，使我们能够在相对假设驱动的方法中探寻感兴趣区之间连接强度的变化。另外，基于节点的方法在描绘人脑功能连接时具有重要作用。描绘连接组学包括识别大脑所有区域之间的功能连接。因此网络建模分析构建全脑区域之间的边连接矩阵用以连接组学分析。然而，清楚地认识到网络建模分析的劣势也是很重要的。网络建模分析最重要的缺点是节点必须在空间上定义好，并且分析过程中的形状和大小都不能改变。如果节点的空间边界不能够准确反映大脑潜在的功能整合，将使得网络建模分析结果无法解释。