4.5.2　时频分析

脑电信号是一个时间信号，每个时刻都含有不同的频率成分。传统的频域分析方法无法体现出时间维度下频率变化的特征，因此出现了基于傅里叶变换、时间与频率结合的二维分析方法，如短时傅里叶变换、小波变换等，使得脑电信号频域的分析更加精确。

1.短时傅里叶变换

在信号处理中，信号的时域信息具有完美的时间分辨率但没有频率信息，而傅里叶变换虽然拥有完美的频率分辨率，却无法定位时间位置，这些缺点使得傅里叶变换不适用于分析时间上局部化的信号，尤其是瞬时信号。鉴于此，1946年Gabor引入了窗口傅里叶变换：

其中，g（t）为选定的窗函数，此窗函数可以有不同的选择，如汉宁窗、海明窗、高斯窗等，通过在时间轴上滑动固定的窗函数，对时域信号进行傅里叶变换，得到各个不同时间窗内的频域信息。但是由于分辨率及时间窗大小在选定窗函数时就已经确定，因此在时间变化过程中不能兼顾时间与频率分辨率的要求。

2.小波变换

短时傅里叶变化可以将频率信息在不同的时间窗中呈现，但时间宽度在所有频率中都是一致的，而在实际情况中低频信息波形相对较宽，因而应选择相对较大的时间窗；相反高频信息则在较小的时间窗中可以获得较高精度，因此短时傅里叶变换不能适应低频信号与高频信号对分辨率的不同要求。1974年，由法国物理学家J.Morlet首次提出了小波变换的概念，将傅里叶变换中无限长的三角函数基，替换为有限长且可以衰减的小波基。小波变换由载波乘以包络组成，公式如下：

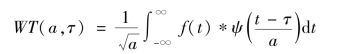
其中，ψ（t）是基小波，包含两个变量：尺度a和平移量τ。尺度a控制小波函数的伸缩，与频率相关；平移量τ控制小波基函数的位移，与时间信息相关。因此小波变化是定义了一个可以伸缩平移的基函数，基函数与信号相乘得到当前尺度下对应的频率成分，由此可以提供自适应的频率-时间维度信息，解决了短时傅里叶变换的问题，实现了高频信号与低频信号的高精度分析。