5.1.1 磁共振基本概念
1.原子核的自旋特性
提到磁共振成像，不得不先提到原子。原子包括原子核和核外电子两部分，其中原子核由带正电的质子和不带电的中子组成，它们几乎提供了原子的全部质量。电子在原子核外围绕原子核运动，在电磁场作用力下按照量子力学的规律运动。原子核的三个基本特征如下：原子核中的质子数（和原子在元累周期表中的序数相同）、原子核质量数（等于质子和中于数之和）以及原子核自旋量子数ћ。原子核自旋如图5.1所示。
由于中子和质子的自旋量子数都等于1／2，因而所有元素的原子核按它们的自旋量子数，分为零、半整数和整数三类。如果质子数和中子数都为偶数，则原子核的质量数必然是偶数，这类原子核的自旋量子数ћ＝0，其核磁矩也为零。这类原子核不和外磁场发生相互作用，而其余的原子核一般都有自旋，因而也都有核磁矩，可以用核磁共振（nuclear magnetic resonance，NMR）技术进行研究。体内氢核1 H的含量最为丰富，对核磁共振成像最为灵敏，现在医用磁共振成像主要采用质子成像。人体内自由水占人体重量的65%～70%，自由水和脂肪中的质子都可以用于磁共振成像。用于描述万高斯场强（Tesla，T）下自旋核共振频率的参数称为旋磁比，用γ表示，单位为MHz／T。除了H元素之外，还有一些元素像是13 C、39 K等，由于其特殊性质也会在其他磁共振研究中使用。表5.1为人体内主要原子核的旋磁比。
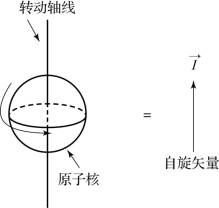
图5.1 原子核自旋
（摘自《脑功能成像物理学》［1］）
表5.1 人体内主要自旋核的旋磁比
我们以1 H的自旋为例，想象质子是一个表面均匀分布正电荷且围绕轴线进行高速旋转的球体，如图5.2所示。旋转过程中质子表面的电荷产生环形电流，产生一个磁场，这个磁场称为核磁矩。对于中子来说，磁矩是由于中子表面和内部的正、负电荷分布的不均匀引起的，使得自旋的中子同样具有微小的磁场，但是与质子本身带有的电荷相比，其电荷量要小很多，旋转之后形成的磁矩也比质子形成的磁矩小得多。1 H原子核自旋的角动量J→与磁矩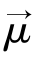
之间的关系如下：
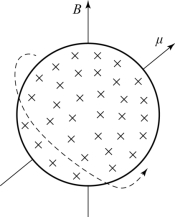
图5.2 自旋质子表面分布的电荷产生磁矩（摘自《脑功能成像物理学》［1］）
其中，γ是旋磁比，h是普朗克常数。
我们研究磁共振时，往往是大量质子的集合，若一个质子的自旋磁矩用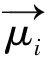
表示，单位组织中的所有自旋磁矩的矢量和（磁化矢量）用
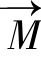表示，即
在没有外加磁场的情况下，各个质子自旋磁矩的方向不同，宏观上相互抵消。在有外加磁场存在时，任意自旋磁矩在磁场中只能取顺磁场方向和逆磁场方向中的一个排列，在磁场方向的投影即Z向分量μz＝±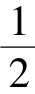
γh，它们合成磁化矢量也必定在Z方向上（Mz）。
2.共振条件与拉莫进动
刚刚提到，无外加磁场的情况下人体内的氢原子核自旋随机取向，不同取向的核自旋形成的磁场相互抵消，导致宏观核磁矩总和为零。但是将质子放到恒定磁场B0中，向样品发射电磁波进行激励。若电磁波的频率v0恰好能够满足关系式：
ΔE是自旋系统中的两个能级之间的能量差。在这一条件下，原来处于低能级的自旋将被激发，跃迁到高能级，这就是一般所说的有自旋特性的原子核与入射的电磁波（场）的核磁共振现象，又称磁共振。
置于恒定磁场B0的自旋磁矩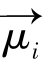
，如果它的矢量方向与外界磁场方向不一致，那么磁矩将受到一个力矩作用，使得磁矩
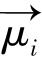的方向不断地变化，磁矩
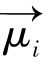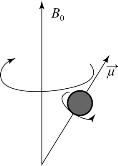
及其在XY平面上的投影绕B0方向以角频率w0旋转，而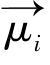
与磁场B0（即Z轴）方向的夹角不变。那么也就是说一个有自旋特性的原子核受到恒定磁场的作用后除绕自身轴线进行自旋外，还将以磁场方向为轴做匀速圆周运动。这种运动被称作拉莫（Larmor）进动，示意图如图5.3所示。进动角频率w0取决于外界磁场磁感应强度B0（静磁场）以及质子的旋磁比γ：
上式是磁共振中一个重要表达式，被称为拉莫方程，它表述了各种有自旋特性的原子核在外加磁场中与入射的电磁波产生的磁共振现象所必需的条件，即在原子种类一定的情况下，激发磁共振所需要的电磁波频率取决于作用于原子核的外加磁场的强度；在外加磁场强度一定的情况下，激发特定原子核的磁共振需要入射特定频率的电磁波且共振频率与原子核的γ值成正比。
3.射频场作用下的自旋磁矩与磁化矢量
前文提到，在均匀磁场中的自旋质子进行拉莫进动，现在向其发射射频（RF）电磁波，那么除了恒定磁场B0外还会有一个射频电磁场作用。该射频场的磁场分量为B1，与B0方向垂直，振动角频率为ω，在旋转坐标系中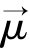
绕B1进动。可以定义一个坐标系X′Y′Z′，它的Z′轴与固定坐标系Z轴重合，X′轴与B1重合，即X′Y′Z′与矢量B1一起以角频率ω进行旋转。当B1变化的角频率与
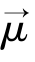进动的角频率相等时，X′Y′Z′坐标系下，恒定磁场B0对磁矩μ→的作用消失，而自旋磁场B1对磁矩
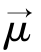起着静磁场的作用，磁矩
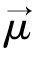必然存在以射频磁场B1为轴的进动，这一进动角频率ω1＝γB1。在射频场B1的作用下，自旋磁矩
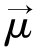围绕射频场B1进动，这将使得它与B0的方向的夹角增大。
图5.3 自旋质子进动示意图（摘自《脑功能成像物理学》［1］）
宏观角度来说，磁化强度矢量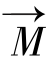
作为许多自旋磁矩
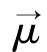的合成，其在射频场的运动如图5.4所示。在恒定磁场中受射频磁场作用，存在两种进动方式：在恒定磁场B0中，若磁化强度矢量
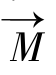由于某种原因偏离B0方向一个角度θ，它便在保持这个角度大小不变的情况下以角频率ω0＝γB0绕B0方向做拉莫进动；施加于B0方向垂直的射频场B1的作用且B1变化的角频等于ω0时，在以角频率w0旋转的坐标系中，磁化强度矢量
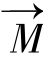将绕B1进动，绕B1进动的角频率ω1＝γB1。倘若射频场作用的起始时刻
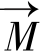处在Z方向，射频场所持续的时间为τ，则时间τ后，
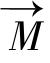偏离Z方向的角度为w1τ。由于τ的持续时间很短，所以这一射频波也被称为射频脉冲（radio-frequency pulse），τ称为脉冲宽度。射频脉冲的命名通常是其引起的磁化矢量的翻转角大小，像是能使磁化强度产生90°翻转角的射频脉冲叫作90°射频脉冲，它的加入可以将磁化矢量
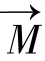从Z方向完全翻转到XY所在的平面。
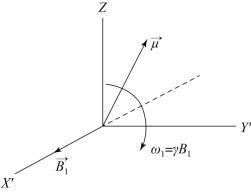
图5.4 在旋转坐标系中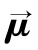
绕B1进动（摘自《脑功能成像物理学》［1］）
综上所述，在射频场的作用下磁化强度矢量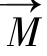
有B0、B1两个方向的进动，在B1的作用下不难得出矢量
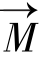与B0之间的夹角将不断增大，其运动轨迹如图5.5所示。
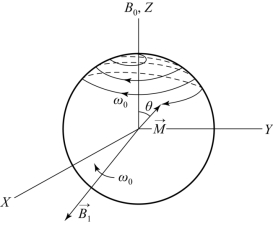
图5.5 磁化矢量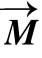
在射频场作用下的运动（摘自《脑功能成像物理学》［1］）
4.纵向弛豫与横向弛豫
由前文可知，当质子集合收到射频脉冲激励时会发生磁共振，平衡状态被破坏，M0偏离Z方向，纵向磁化强度Mz随之减少，同时出现磁化强度的横向分量Mxy。停止射频脉冲后，质子系统开始弛豫，即由不平衡态向平衡态恢复。
由于非平衡态时磁化强度不仅有纵向分量还有横向分量。那么磁化强度恢复平衡状态的过程就包括纵向分量向M0恢复以及横向分量向0恢复的过程。据此，弛豫可以分为纵向弛豫和横向弛豫。
我们首先将热平衡条件下两个能级的质子数之差用ΔN0表示，相应的磁场强度用M0表示。纵向磁化强度从某个Mz向热平衡值M0恢复的过程叫作纵向弛豫过程。这一变化过程可用下面的微分方程描述：
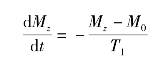
这里T1是一个由物质本身性质决定的特征时间，称为自旋-晶格弛豫时间，也称为纵向弛豫速率的特征时间，人体不同组织具有不同的T1。
将弛豫过程的开始时刻记作t＝0，Mz的值为Mz（0），则
如果t＝0时Mz（0）＝0，上式化为
以直角坐标系下的曲线描绘上式，如图5.6所示。
横向弛豫时间可以类比纵向弛豫的方法进行描述：
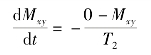
这里T2是横向弛豫速率的特征时间。类比上文对Mz的求解可知Mxy＝Mxymax e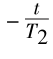
。其中Mxymax是横向弛豫开始时刻横向磁化磁化强度Mxy的最大幅度。如果是一90°射频脉冲进行激励，那么Mxymax＝M0。图5.7是Mxy与时间的关系曲线。
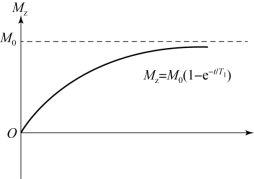
图5.6 纵向弛豫曲线
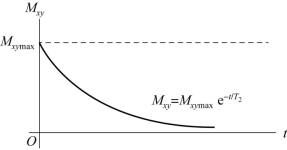
图5.7 横向弛豫曲线