4.5.1 非线性动力学方法
大脑可以被看作一个非线性动力学系统，脑电信号是其输出，具有非线性动力学特征。1985年，Babloyantz等首次将非线性动力学和混沌理论应用于脑电信号分析。目前非线性动力学方法主要有Lorenz散点图、Lyapunov指数、相关维数、复杂度等［12］。
1.Lorenz散点图
假设脑电信号的采样点为x（1），x（2），…，x（n），…，Lorenz散点图的绘制是采用相邻两采样点的前一点值为横坐标（X轴），后一个采样点为纵坐标（Y轴），即
｛（x，y）｜x＝x（n），y＝x（n+1），n＝1，2，3，…｝
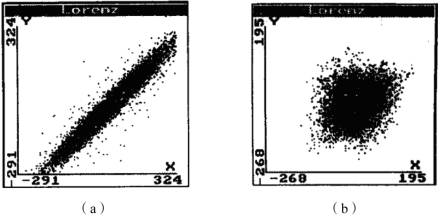
Lorenz散点图比较直观，可以看出相邻采样点之间的关系和信号的幅值。一般癫痫病人的Lorenz散点图沿着45°线分布，正常人则分布在小范围的椭圆形区域内，如图4.11所示，说明癫痫病人脑电信号相邻点较为接近，而正常人的信号比较稳定。Lorenz散点图对脑电信号进行粗略的分析，呈现直观的图像特征，并未量化分析。
图4.11 癫痫病人与正常人的Lorenz散点图（摘自《脑电信号的几个非线性动力学分析方法》［13］）
（a）癫痫病人的Lorenz散点；（b）正常人的Lorenz散点图
2.Lyapunov指数
混沌系统是指在一个确定性系统中存在着貌似随机的不规则运动，此系统行为具有不确定性、不可重复性及不可预测性，并且未来状态对初始值具有敏感的依赖性。混沌是非线性动力系统的固有特性。Lyapunov指数用于判断一个系统是否属于混沌系统，即描述初始状态的微小不确定性扩大率的重要参数。当系统Lyapunov指数存在正值时，表明系统具有混沌特征。研究者们计算了脑电信号的最大Lyapunov指数，结果均为正值，证实脑电信号具有混沌特征。
3.相关维数
相关维数用于描述系统的自由度，是混沌时间序列分析中根本的量化指标之一。在条件不变的情况下，脑电信号的变化反映了大脑活动的细微变化。相关维数为1时，系统呈现周期振动；相关维数为2时，系统存在两个不可约的频率的周期振荡；相关维数边界不是整数时，系统处于混沌运动状态。