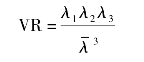5.4.1 弥散张量成像的物理基础
1.弥散
分子扩散（弥散）是指分子的随机平移运动，也称布朗运动，是由分子所携带的热能引起的运动。水分子在扩散磁共振成像研究中最为常见。水在与内部结构对齐的方向上扩散得更快，在垂直于上述方向时扩散得更慢。
2.弥散张量
分子从起始位置经过指定时间间隔后漂移的距离用弥散张量D表示，其矩阵表述如下：
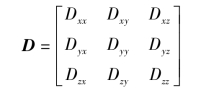
对于均匀介质，弥散系数D是一个标量，反映的是组织扩散的各向同性，也就是说在均匀介质中分子向各个方向运动的概率相同。但是对于非均匀的（各向异性，弥散具有方向依赖性的）介质，如白质纤维束中，扩散系数取决于神经纤维束的走向，那么其扩散张量就要采用上述矩阵表示。对于扩散张量矩阵进行对角化处理，可以得到3个特征值（λ1、λ2和λ3）和对应的特征矢量（e1、e2和e3）：
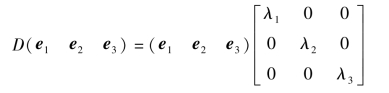
在各向异性组织中，在给定扩散时间情况下，分子扩散形成一个椭球。这一椭球的半径与特征值成正比，椭球的空间走向由特征矢量决定。特征值、特征矢量与扩散椭圆的关系如图5.20所示。
在研究脑白质纤维走向时，我们将特征值降序排列（λ1≥λ2≥λ3），最大特征所对应的特征矢量方向就是神经纤维的走向，沿着线位的走向扩散率大于垂直的纤维走向。白质的各向异性明显大于灰质，二者的扩散张量椭球如图5.21所示，可以看出，灰质也并不完全是各向同性。所以在追踪白质纤维时会对各向异性设置一个阈值。
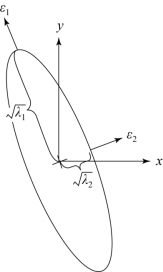
图5.20 特征值、特征矢量与扩散椭圆的关系（摘自《脑功能成像物理学》［1］）
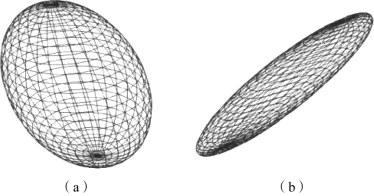
图5.21 灰质、白质扩散椭球示意图（摘自《脑功能成像物理学》［1］）
（a）灰质；（b）白质
3.常见导出量
将3个特征值进行不同的组合可以得到不同的变量，常见的变量包括以下几个。
平均扩散率（mean diffusivity，MD）代表扩散椭球的平均半径：
相对各向异性（relative anisotropy，RA）计算的是特征值的方差与平均值的比值：
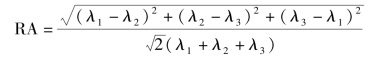
各向异性比值（fractional anisotropy，FA）可以形象地理解为扩散椭球“椭”的情况，FA越大，椭球越扁长。它是扩散张量的各向异性成分与整个扩散张量的比值：
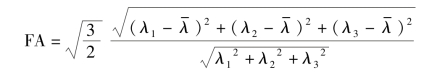
根据上式可以看出，当λ1＝λ2＝λ3时，FA＝0，当λ1≫λ2≫λ3时，
，FA近似于1。所以FA的取值范围是0～1，FA与扩散的各向异性成正比。
容积比（volume ratio，VR）等于扩散椭圆体积与半径为平均扩散率的球的体积之比：
