3.1.3 几种较新的去噪方法
多源图像的去噪方法有许多种，但是随着新问题的不断出现而使学者们研究出了许多新的去噪方法。例如，基于阈值的小波变换的去噪方法、基于模糊加权均值的去噪方法、基于形态学开闭运算的去噪方法等。
1.基于阈值的小波变换的去噪方法
多源图像经过基于小波变换的去噪算法处理后，其图像中幅值较大的小波系数一般为有用信号，而幅值较小的小波系数一般情况下是噪声信号，因此选择一个最佳的阈值进行阈值处理小波系数，就可以把有用信号的系数保留下来，同时去除大部分的噪声系数，甚至将噪声系数减小到零，从而完成去噪处理。
基于阈值的小波变换的去噪方法，就是对有噪声的图像先进行一次小波变换，得到几个分量，分别用W1yj，（k，l）、W2yj，（k，l）、W3yj，（k，l）来表示，用HLj（k，l）、LHj（k，l）、HHj（k，l）来表示其高频分量，将这些分量作为小波系数，其中（k，l）为二维小波变换系数，j=1，2，…，Jm表示分解层次。得到的低频分量LLj（k，l）用W0ym，（k，l）表示，且认为LLJ（mk，l）=W0ym，（k，l），设计算得到的阈值为λ。通常采用的阈值法有假设检验法、最大限度地减少风险阈值的方法、贝叶斯收缩阈值法。一般采用通用的阈值法：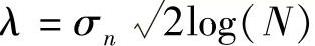
，其中N是图像中小波系数的总数，σn是噪声的标准差。一般采用噪声标准差鲁棒中的估计值σn为MAD/0.6745，这里的MAD代表对原图像的第一次小波分解获得的小波系数的中值。一般情况下采用直接阈值法对小波变换系数Wiyj，（k，l）（其中i=0，1，2，3；j=1，2，3，…，Jm）进行阈值处理。主要有以下两种方式。
（1）硬阈值法
先对噪声图像实施小波变换，忽略不计粗尺度信号，只对细节信号做阈值处理，当某个位置小波变换值小于阈值时将其置零，大于阈值时将其保留原值。其表达式为
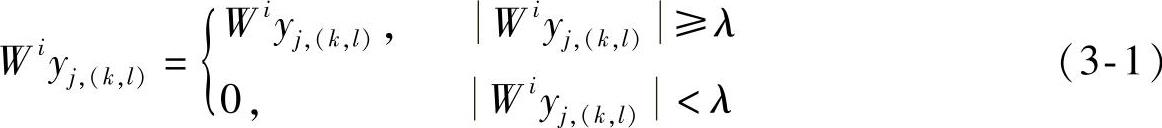
最后，利用小波变换重构，求出去噪后的图像。
（2）软阈值法
先对噪声图像实施小波变换，并求得带有噪声的小波系数，再将细节信号阈值化处理。当小波变换在图像中的位置值小于阈值时将被设置为零，并且当小波变换位置值大于阈值时，进行以下运算，其中sgn（x）为符号函数。
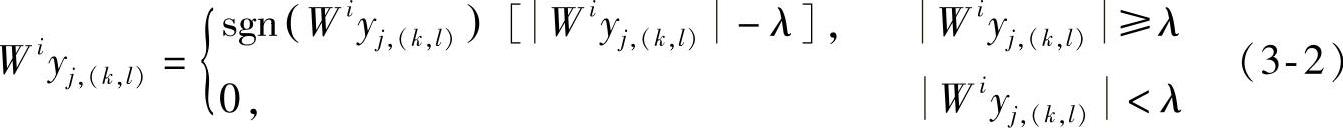
最后对小波系数Wiyj，（k，l）的估计值W^iyj，（k，l）做小波变换的反变换以重建图像，得到去噪后的图像。
2.基于模糊加权均值的去噪方法
基于模糊加权均值的去噪方法依赖于模糊隶属度函数的概念，对加权均值优化处理，使其不仅能有效地降低高斯噪声，同时也对混合噪声及脉冲噪声有较好的抑制能力。该方法的优点是既能保护图像的边缘信息，也能有效地减弱边缘模糊现象。
3.基于形态学开闭运算的去噪方法
基于形态学开闭运算的去噪方法的基本思想是借助数学形态学，用特定形态的元素去衡量并提取与之相应的原图像中的形状，当结构元件移动到原始图像，我们可以研究图像中各部分的相互关系，以了解图中各部分的结构特点，区分有用的图像信息和图像信息的噪声，为了达到目的，从而完成去噪处理。因此，该方法去噪效果主要依赖于其结构元素的选取。常用的结构元素包括：圆形、方形、菱形、六边形、线段等。目前没有特定的方法选取结构元素，只能根据图像要求的处理结果及图像本身特征来决定。
数学形态学是由一组形态学基本的代数算子构成，它的基本运算包含：开、闭运算，腐蚀，膨胀。
集合B腐蚀集合A表示为AΘB，其定义为
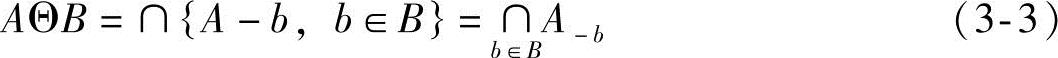
通过腐蚀运算对图像进行腐蚀操作后，若所有结构元素均为正值，则输出图像比输入图像偏暗；若输入图像的细节小于结构元素的区域，则细节亮的效果会被削弱。因此，腐蚀运算能够使图像边界向内部紧缩及消除边界点的特征。
腐蚀的对偶操作是膨胀，集合B膨胀集合A表示为A㊉B，其定义为
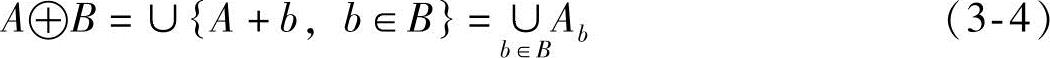
膨胀运算对图像进行膨胀操作后，若所有结构元素均为正值，则输出图像比输入图像偏亮，与此同时暗细节的效果会被减弱。因此，膨胀运算能够使图像边界向外部扩张。
基于腐蚀和膨胀运算可以推导出各种数学形态学的基本运算。开运算和闭运算就是这两种运算的组合运算。集合B对集合A的开运算就是先做腐蚀运算后做膨胀运算，表示为A。B，其定义为
A。B=（AΘB）㊉B（3-5）
开运算的优势体现在能够去除比结构元素要小的突出的亮点噪声，并且能够维持图像整体区域的特征以及大部分的灰度层级。开运算的对偶运算是闭运算，集合B对集合A作闭运算就是先做膨胀运算再做腐蚀运算，表示为A·B，定义为
A·B=（A㊉B）ΘB（3-6）
闭运算的优点是不仅能够在不明显改变物体的形状和面积的前提下对图像做去噪处理，而且能够在连接邻近物体的同时填充图像内部的细小空洞。因此，对同一幅图像使用相同的结构元素做形态学开闭运算的去噪处理，闭运算能够起到削弱膨胀运算对边界扩张的作用；而开运算则能够起到补充被腐蚀消除的部分图像的作用。因而形态学开闭运算的去噪方法具有良好的去噪效果和保持清晰的目标轮廓的优点，与其他去噪算法相比，它的这个优点更为显著。
图像质量评价中的主观评价也是人类视觉特性，但评估质量受人为因素的影响，不能准确地描述图像的定量分析，因此本章采用图像的两种主要的客观评价来比较基于阈值的小波变换的去噪方法、基于模糊加权均值的去噪方法、基于形态学开闭运算的去噪方法这几种新的去噪方法的优劣。采用的两种主要的客观评价方法是峰值信噪比（PSNR）和信噪比（SNR），其中峰值信噪比可定量描述对图像的去噪质量；信噪比用来比较含噪声的原图像与去噪后图像的质量，信噪比越大，图像品质就越好。表3-1列出了几种较新的去噪方法的峰值信噪比和信噪比。
表3-1 几种较新的去噪方法的峰值信噪比和信噪比（单位：dB）
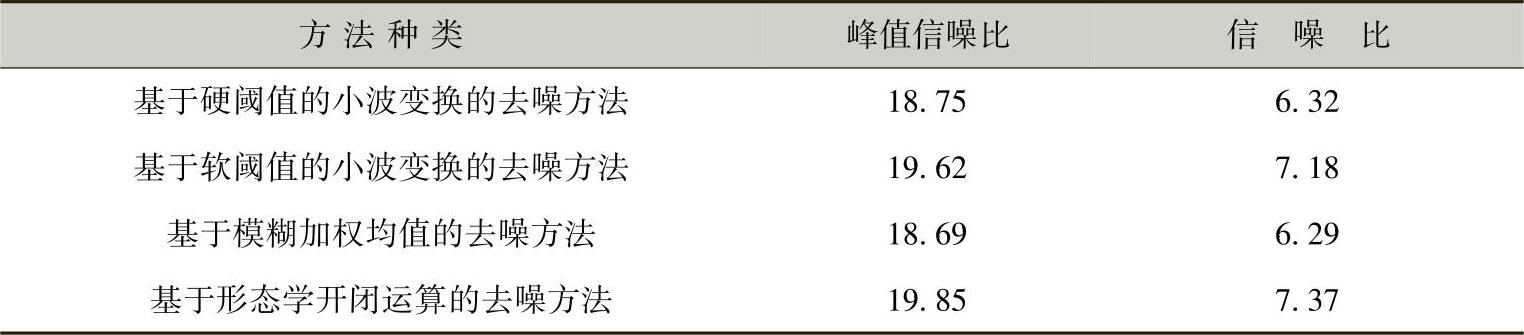
因此，由表3-1中的数据可知，基于模糊加权均值的去噪方法的峰值信噪比和信噪比是最低的，而基于形态学开闭运算的去噪方法的峰值信噪比和信噪比是最高的。因而，相对于其他去噪方法，采用基于形态学开闭运算的去噪方法得到的图像去噪质量较高、效果较好。
本章采用了基于形态学开闭运算的去噪方法对多源图像做去噪处理，使得多源图像在被分水岭算法分割之前不仅消除了无规则的明暗噪声和细节扰动，而且也消除了易导致过分割的区域噪声与细节，更重要的是使多源图像的重要轮廓得以保留。因此，此形态学开闭运算去噪方法对改进分水岭算法起到了关键作用，它使分水岭分割算法对图像中噪声敏感的缺陷有所改善，更为重要的是它使分水岭算法分割前输入的多源图像具有正确的轮廓信息，即对修正多源图像起到了关键作用，为分水岭算法正确、有效的分割奠定了一定的基础。
采用了基于形态学开闭运算的去噪方法对分水岭算法的改进，不仅是利用它的去噪处理改善多源图像的输入质量，更重要的是利用它对多源图像去噪的同时也将多源图像进行梯度化处理，将多源图像变成它的梯度图输出。因为分水岭算法的基本思想来源自地理学，将被分割图像视作地形图并求取梯度图像，因此采用基于形态学开闭运算的预处理恰好是分水岭分割前的第一步，即图像梯度化处理。传统的梯度化处理方法是通过微分算子，例如Sobel、Prewitt、Canny等求得梯度图。而本章选用形态学开闭运算的图像即为梯度图像，是因为形态学梯度运算有非线性的特点，能够加强图像中极值对比度，并且能够保护图像中目标轮廓的区域。
本章采用VC++6.0开发环境编程调试完成形态学开闭运算的去噪算法，实验结果如图3-1和图3-2所示。其中图3-1为可见光图像的形态学开闭运算去噪后的图像，图3-2为红外图像的形态学开闭运算去噪后的图像。
图3-1 可见光图像去噪后的图像
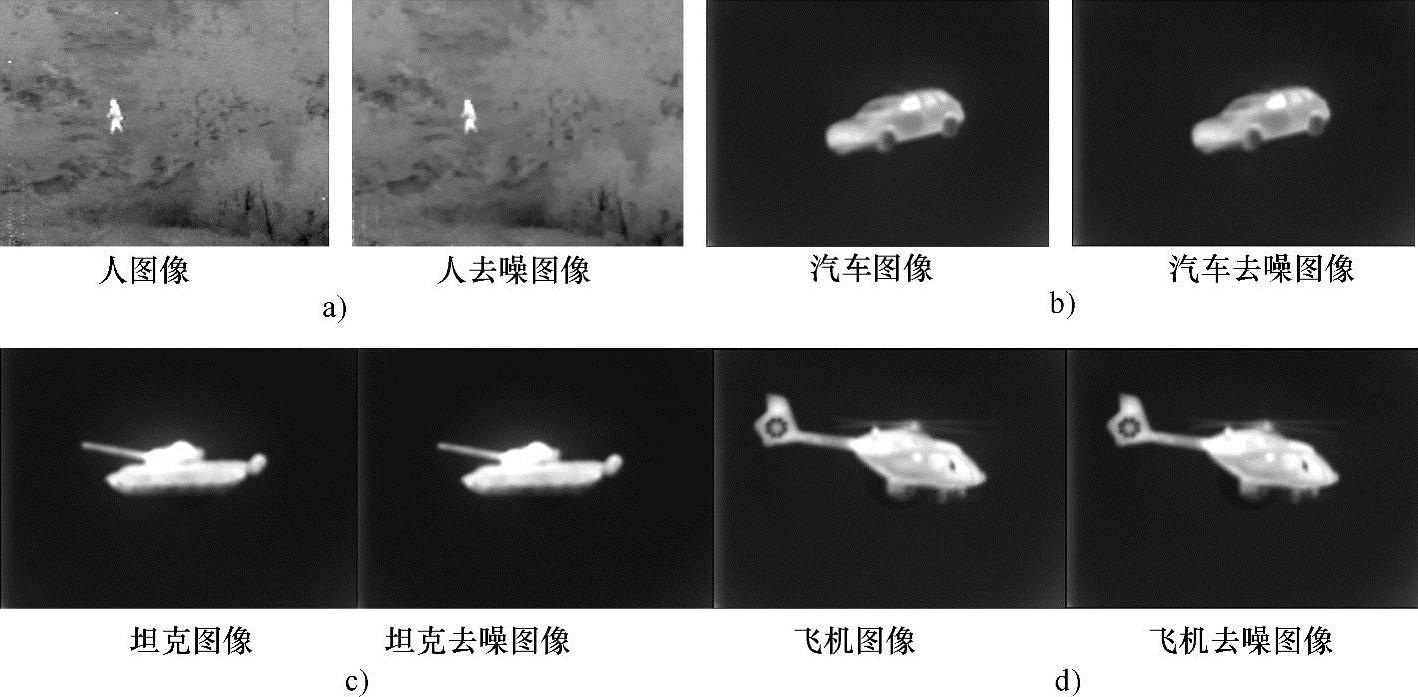
图3-2 红外图像去噪后的图像