8.3.2  数学模型

8.3.2 数学模型

根据方差最大化原理，用一组新的、线性无关且相互正交的向量来表征原数据矩阵的行或者列，这组原数据向量的线性组合即为主成分。

设有n个样品，每个样品观测p个指标，这p个指标构成的p维向量分别为X₁，X2，…，X_p，得到原始数据资料阵：

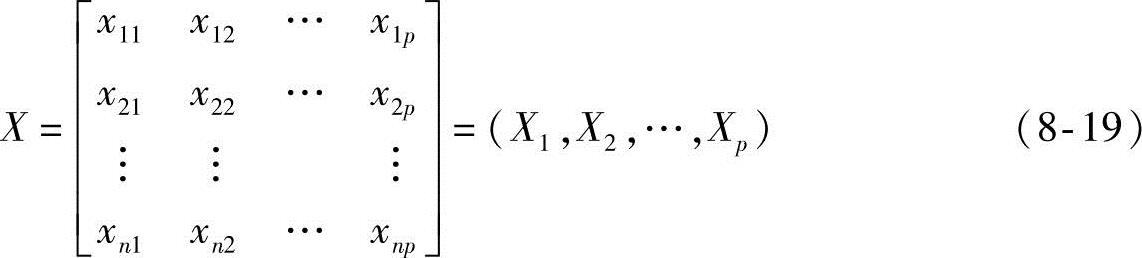
式中，。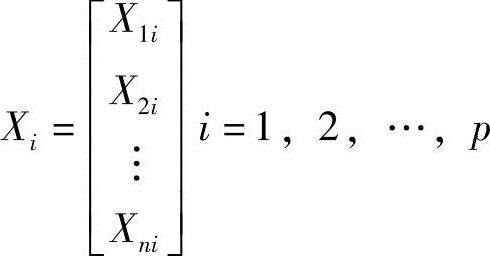

设数据矩阵X的均值为_μ，协方差矩阵为Σ。将X的p个指标X₁，X₂，…，X_p作线性组合，形成新的综合指标，即

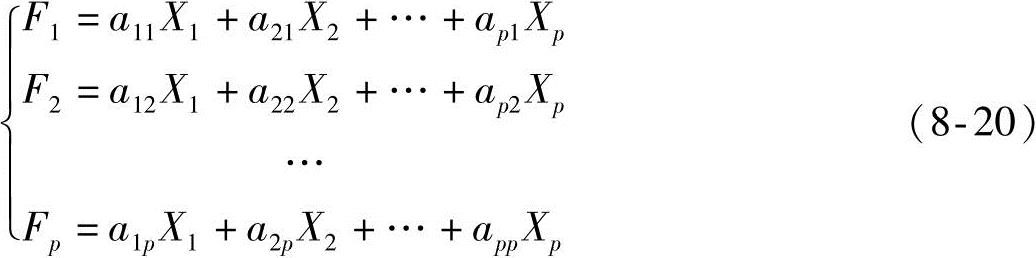
简写成：

F_i=a_1iX_i+a_2iX₂+…+a_piX_p，i=1，2，…，p（8^-21）

若线性变换满足以下约束：

1）a_i′a_i=1，即a²_1i+a²_2i+…+a_p²i=1，其中i=1，2，…，p。

2）F_i与F_j（i≠j，j=1，2，…，p）互不相关。

3）F₁是X₁，X₂，…，X_p的一切线性组合（系数满足上述方程组）中方差最大的，F₂是与F₁不相关的X₁，X₂，…，X_p一切线性组合中方差最大的，…，F_p是与F₁，F₂，…，F_p-1都不相关的X₁，X₂，…，Xp^一切线性组合中方差最大的。

那么，称式（8-20）为指标X₁，X₂，…，X_p的主成分分析模型，并将式（8-20）确定的综合指标F₁，F₂，…，F_p分别称为原始指标的第一，第二，…，第p个主成分。

主成分，从代数学的观点看就是p个随机变量X₁，X₂，…，X_p的一些特殊的线性组合，而在几何上这些线性组合代表以X₁，X₂，…，X_p构成的坐标系经过平移、尺度伸缩和坐标旋转产生的一个新坐标系，新坐标轴为样品偏差最大的方向（或者说具有最大的样品方差）。为了能够更直观地理解主成分分析的基本思想，下面以最简单的二元正态变量来讨论主成分分析的几何意义，所得结论可以很容易地扩展到多维的情况。

设有n个样品，每个样品有p个观察变量，记为X₁，X₂，…，X_p，它们的综合变量记为F₁，F₂，…，F_p。当p=2时，由变量是X₁，X₂组成的坐标空间中，n个样品散布的情况如图8-2所示。

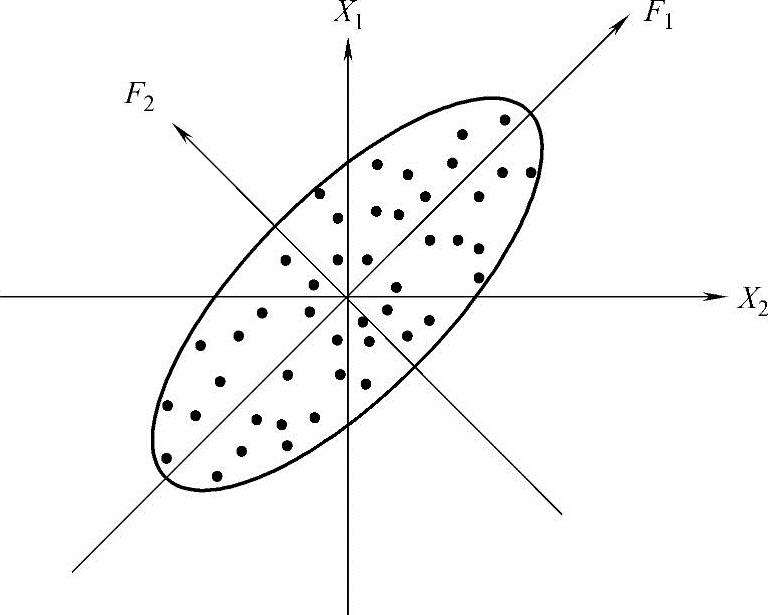
图8-2 主成分的意义

由图可以看出，n个分散的点大致形成一个椭圆。若在椭圆长轴方向取坐标轴F₁，在短轴方向取F₂，这相当于将坐标轴按逆时针方向旋转θ角度，根据旋转轴变换公式，新老坐标之间有如下关系：

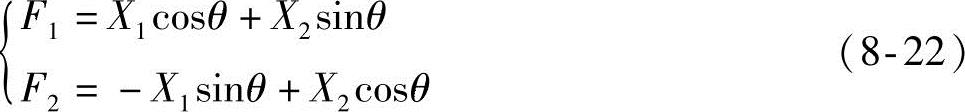
其矩阵形式为

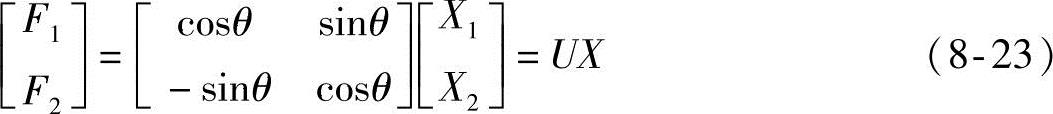
式中，U为旋转变换矩阵，由式（8-23）可知U为正交阵，即满足U^T=U^-1，U^TU=I。

从图8-2可看出，经过旋转后的n个点的波动（可用方差表示）大部分可以归结为在F₁轴上的波动，而在F₂轴上的波动较小。当图8-2椭圆相当扁平的时候，那么我们可以只考虑F₁方向上的波动，而忽略F₂方向的波动。这样，二维就可以降为一维，只取第一个综合变量F₁即可，即椭圆的长轴。一般情况下，p个变量组成p维空间，n个样品就是p维空间的n个点，对p元正态分布变量来说，找主成分的问题就相当于找p维空间中椭球体的主轴问题。