13.2.5 核函数
对于非线性问题，支持向量机通过一个映射过程将原始空间中的问题映射到更高维度的空间中，使之在高维度空间中成为一个线性问题，并在高维度空间中进行求解。但是，由于维数急剧增长，通常情况下在特征空间计算最优分类面往往很难实现。但是，在求解支持向量机的对偶问题过程中，仅在高维空间中的点积运算，如果能找到一个合适的函数K（xi，xj），使得
K（xj，xj）=φ（xi）·φ（xj） （13-22）这样，在高维特征空间中的内积运算就可以在原空间中利用函数来实现，避免了维数转换。函数K（xj，xj）就称为核函数（Kernel Function）。
支持向量机的核函数种类繁多，不同的核函数可以满足不同算法的需要，但是基本所有的核函数都会满足Mercer条件：
K（x，x′）为连续对称核，其中x和x′的取值范围为区间[a，b]。那么该对称核K（x，x′）可以展开为下式中的级数形式：
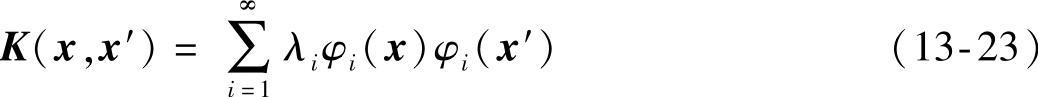
式中，φi（x）为特征函数展开式，λi称为特征值。如果特征值全都是正数，那么称核K（x，x′）是正定核。
式（13-23）满足展开式的合理性和绝对一致收敛性的充要条件为
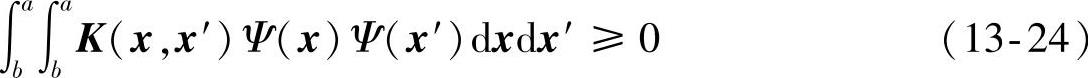
对于所有满足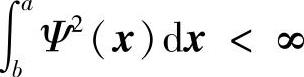
的Ψ（x）成立。
通过Mercer定理我们只能得知该候选核函数是否可以表示高维空间的内积以及是否可以应用于支持向量机。但是它并没有告诉我们如何去构造函数φI（x），因此我们需要自己构造，目前常用的核函数有：
（1）多项式核函数（Polynomial Kernel）：
K（x，xi）=[（x·xi）+1]q （13-25）式中，q为阶数。多项式核函数的优点较多，主要的优点有：全局性能较好、外推能力较强，其中阶数q与外推能力成反比。
（2）径向基核函数（RBFKernel）
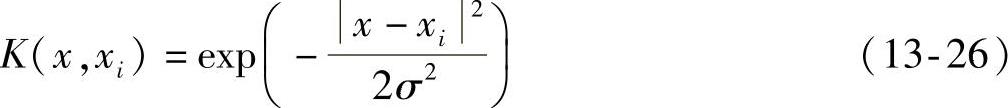
径向基核函数具有很好的局部性，也是运用最为广泛的核函数之一。其中公式中的参数σ对分类器影响较大，其值将直接对分类器的分类能力起到关键性的影响。因此，选取合适的参数在实际应用中是非常重要的环节。
（3）S形核函数
K（x，xi）=tanh（v（x·xi）+c） （13-27）
基于S形核函数的支持向量机可以看作一个含有隐含层的多层感知机。而且可以由算法自动确定隐含层内部的节点数，不需要人为设置，所以这是S形核函数的一个优点。另外，具有全局极小值并可以避免局部极小值也是S形核函数的一个重要优点。