11.2.2  典型相关的定义及导出

11.2.2 典型相关的定义及导出

设有两组相互关联的随机向量X′=[X₁，X₂，…，X_p]和Y′=[Y₁，Y₂，…，Y_q]，U_i、V_i分别为在两组变量内选取的几个具有代表性的综合变量，每个综合变量都是原变量的一个线性组合，如下所示：

U_i=a_i1X₁+a_i2X₂+…+a_ipX_p=a′X（11-4）

V_i=b_i1Y₁+b_i2Y₂+…+b_iqY_q=b′Y（11-5）

CCA要做的工作就是要找到一对投影方向a、b，使得投影U_i=a′X和V_i=b′Y之间具有最大的相关性，这种相关被称为典型相关。U₁=a′₁X，V₁=b′₁Y为X、Y的第一对典型相关变量，类似地可以求出第2对（U₂，V₂），第3对（U₃，V₃），…，第i对（U_i，V_i），而且每对典型相关变量之间互不相关。利用这些典型相关变量就可以反映出X与Y之间的线性相关情况。

一般地，投影方向a与b通过最大化U与V之间的相关系数ρ获得。

由于随机变量U、V与任意常数相乘并不改变它们之间的相关系数，所以为防止结果重复，令

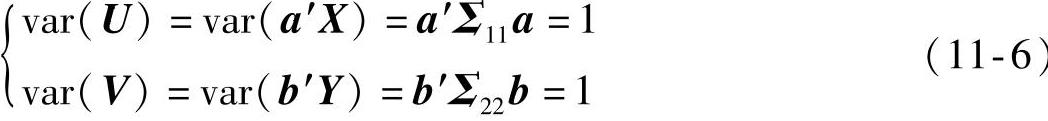
所以

ρ=cov（a′X，b′Y）=a′cov（X，Y）b=a′Σ₁₂b（11-7）

于是求解问题即为在式（11-6）约束下，求出a∈R^p，b∈R^q使得式（11-7）达到最大。

根据拉格朗日定理可将问题转化为求

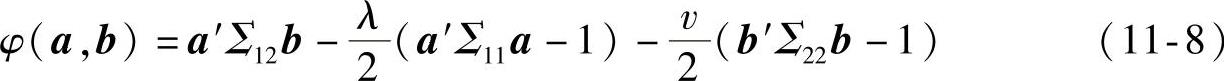
的极大值，其中λ、v是拉格朗日乘数。

根据求极值的必要条件，得

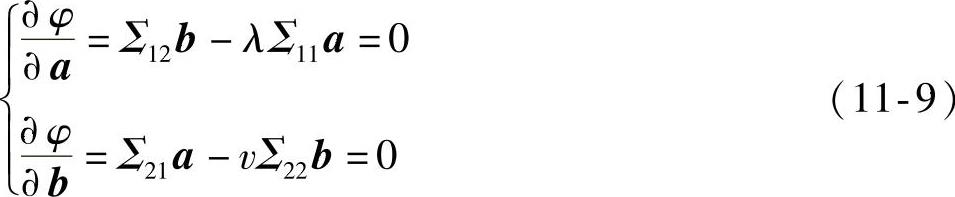
将式（11-9）的两式分别左乘a′与b′，则得

即有

因为（b′Σ₂₁a）=a′Σ₁₂b，所以λ=v=a′Σ₁₂b，可知λ为线性组合U、V的相关系数。用λ代替式中的v，则式（11-11）写为

假定各随机变量协方差矩阵都有逆矩阵，则由式（11-12）中的第二式可得

将式（11-13）代入式（11-12）的第一式，得

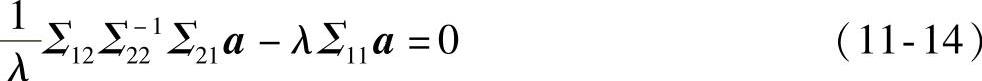
即有

Σ₁₂Σ₂^-21Σ21a^-λ2Σ₁₁a=0（11_-15）同理，由式（11-12）可得

Σ₂₁Σ₁^-11Σ12b^-λ2Σ₂₂b=0（11_-16）用Σ₁^-11和Σ₂^-21分别左乘式（11-15）和式（11-16），得

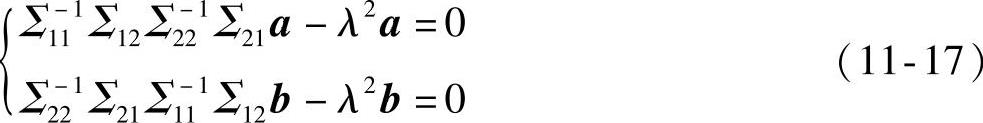
即

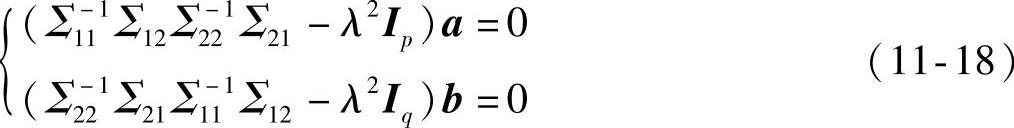
由上述分析可知，Σ₁^-11Σ₁₂Σ₂^-21Σ₂₁和Σ₂^-21Σ₂₁Σ₁^-11Σ₁₂具有相同的特征根λ²，a、b是其特征根对应的特征向量。特征根λ即为我们要求的典型相关系数，a、b为典型相关向量。

由于我们所求的是最大特征根及其对应的特征向量，因此，最大特征根λ²₁对应的特征向量a₁=（a₁₁，a₁₂，…，a_1p）′和b₁=（b₁₁，b₁₂，…，b_1q）′就是所求的典型变量的系数向量，即可得

U₁=a′₁X=a₁₁X₁+a₁₂X₂+…+a_1pX_p（11-19）

V₁=b′₁Y=b₁₁Y₁+b₁₂Y₂+…+b_1qY_q（11-20）式中，U₁、V₁被称为第一对典型变量，最大特征根的平方根λ₁为两典型变量的相关系数，称为第一典型相关系数。

第二对典型变量U₂=a₂′X和V₂=b₂′Y需要满足如下约束条件：

D（U₂）=a₂′Σ₁₁a₂=1

D（V₂）=b₂′Σ₂₂b₂=1（11-21）

另外，为了有效测量两组变量之间的相关信息，第二对典型变量应不再包含第一对典型变量中已有的信息，因此，需要增加约束条件：

cov（U₁，U₂）=cov（a′₁，X，a₂′X）=a′₁Σ₁₁a₂=0

cov（V₁，V₂）=cov（b′₁Y，b₂′Y）=b′₁Σ₂₂b₂=0（11-22）

λ₂为第二典型相关系数。

如此下去，依次可求出第r对典型变量：U_r=a_r′X和V_r=b_r′Y，其系数向量a_r和b_r分别为矩阵Σ₁^-11Σ₁₂Σ₂^-21Σ₂₁和Σ₂^-21Σ₂₁Σ₁^-11Σ₁₂的第r特征根λ²_r对应的特征向量，λ_r即为第r典型相关系数。

综上所述，计算典型相关变量和典型相关系数就是要求解矩阵A和B的特征根及相应的特征向量。若矩阵Σ₁^-11Σ₁₂Σ₂^-21Σ₂₁和Σ₂^-21Σ₂₁Σ₁^-11Σ₁₂的秩为r，则共有r对典型相关变量，r个典型相关系数。