8.1.1  灰度共生矩阵

8.1.1 灰度共生矩阵

灰度共生矩阵是建立在估计图像的二阶组合条件概率密度函数基础上的统计方法，主要描述纹理基元或局部模式随机和空间统计特征，以表示区域的一致性及区域间的相对性。它能反映出图像灰度关于方向、相邻间隔、变化幅度的综合信息，是当前人们公认的一种重要的纹理分析方法。

灰度共生矩阵描述的是在某方向上间隔一定距离的一对像素点对灰度出现的统计规律，即从图像灰度值为i的像元（x，y）出发，统计与其距离为d、方向为θ、灰度值为j的像元（x+a，y+b）同时出现的概率p（i，j，d，θ），其数学表达为

p（i，j，d，θ）={[（x，y），（x+a，y+b）]f（x，y）=i，f（x+a，y+b）=j} （8-1）式中，x=0，1，2，…，N_x，y=0，1，2，…，N_y，i∈[0，L-1]，j∈[0，L-1]。θ为灰度共生矩阵的生成方向，通常取0°、45°、90°、135°四个方向。N_x、N_y分别表示水平和垂直方向的像素总值，L为图像的灰度级。

以下是一个灰度共生矩阵的生成例子。图8-1a所示是一个灰度级为4的图像。由于图像的灰度级决定了共生矩阵的大小，所以共生矩阵为4×4的矩阵。行表示i的灰度变换，列表示j的灰度变换。由式（8-1）可以计算出d=1时0°、90°、135°和45°的灰度共生矩阵P_H、P_V、P_LD、P_RD，如图8-1b所示。

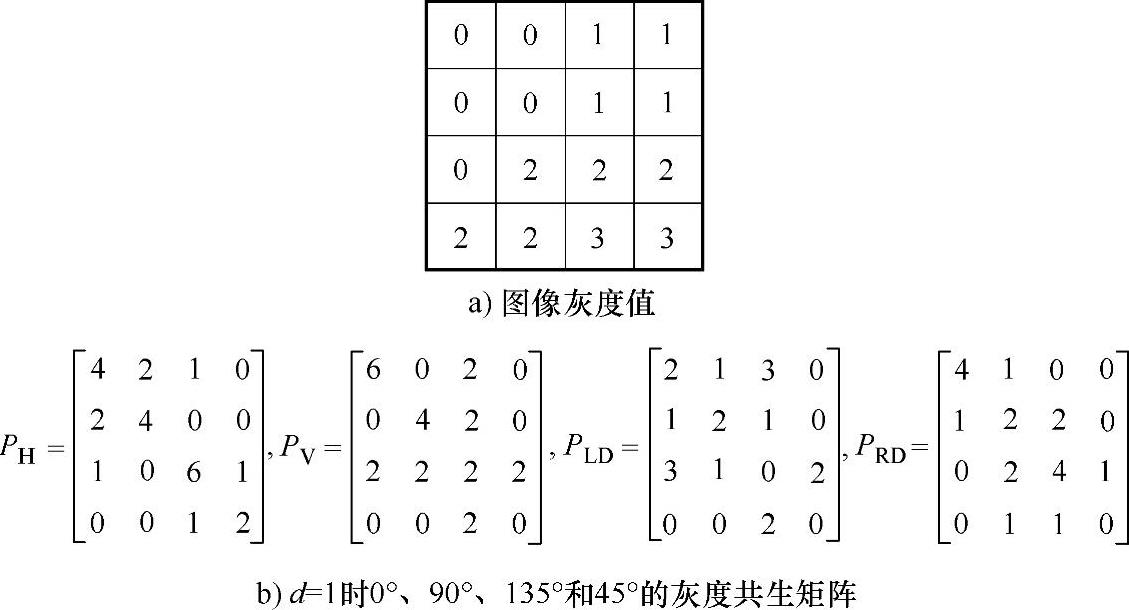
图8-1 图像灰度值和灰度共生矩阵

Haralick等人定义了14个用于纹理分析的灰度共生矩阵特征参数，虽然这14种特征参数都能表达纹理的某些特定信息，但存在信息冗杂、重复表述的问题。根据各个参数的意义，选用以下四个参数：

能量

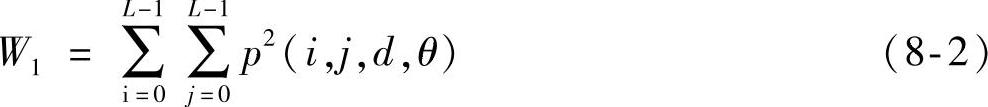
熵

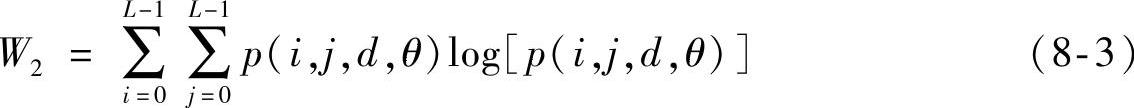
惯性矩

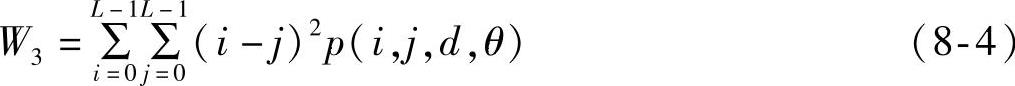
局部平稳性

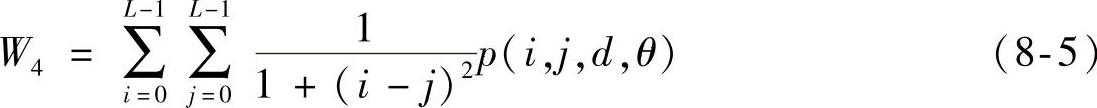
式中，L为图像灰度级，为保证参数的旋转不变性，取0°、45°、90°和135°四个方向参数的均值作为灰度共生矩阵的值。