12.1.2 BP神经网络结构
在BP神经网络的结构中，它主要是由三部分组成，即输入层、隐层和输出层，每层中都包含了大量的神经元，该神经元模型可以用图12-1来描述。
根据图12-1可知，其中x1，x2，…，xn表示神经元的输入量，w1，w2，…，wn表示网络结构层之间的权值，简单地说就是层之间连接的强弱；输入量对应权值的和为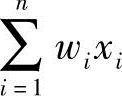
，它代表神经元的激活值，当这个值大于神经元自身的阈值θ时，此时神经网络就可以学习训练了；O表示神经元最终的输出量。那么根据上述介绍，此时输出量就可以用下面的公式来表示，即
在式（12-1）中，函数f代表神经元内输入与输出之间的关系，一般称这样的函数为激活函数或者是输出函数。在神经元内，我们可以用W来作为神经元中相应的权值量，用X表示神经元的输入量，它们可以分别用下式来表示：
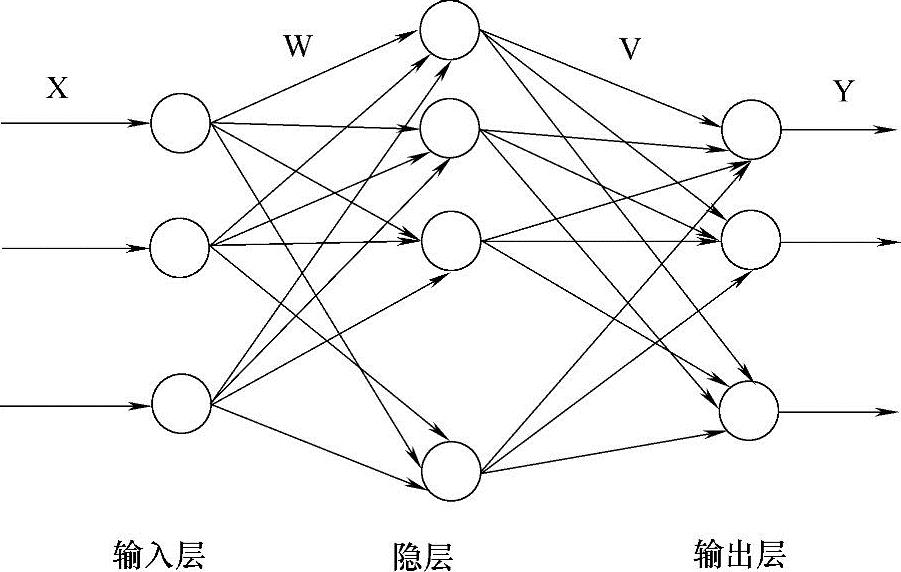
图12-1 BP神经网络结构图
我们可以通过对激活值进行假设，即net=WTX，类似于我们对神经元进行外部刺激来影响神经元内部反应。此时式（12-1）可简化为f（net-θ）。在实际使用中，存在很多类型的激活函数，但是一般常用的有这么几种，即S（Sigmoid）形函数、阈值函数和双面正切函数，它们的函数图如图12-2所示。
阈值函数，该函数公式如下：
S形函数，该函数公式如下：
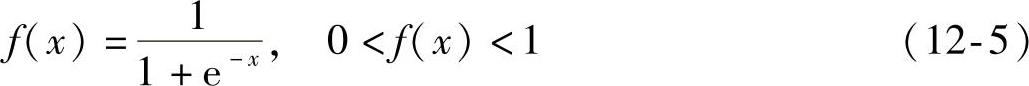
双面正切函数，该函数公式如下：
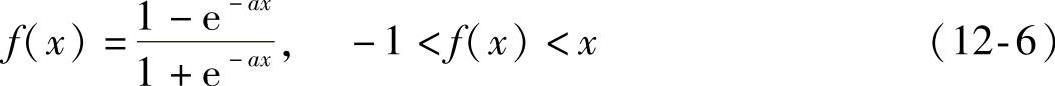
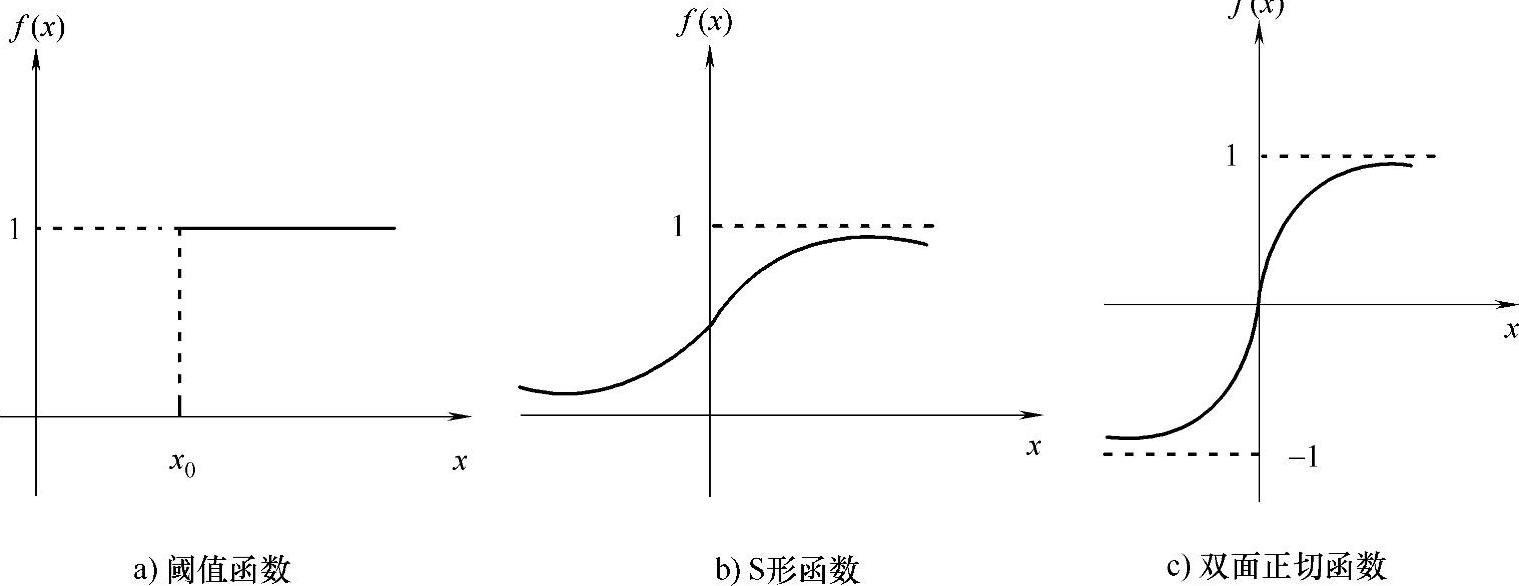
图12-2 常用激活函数图
在对BP神经网络的隐层函数设计和进行选取时，一般都是选用S形函数，因为其可导，容错性比较强，而且它还能对信号的增益有非常好的控制能力。在式（12-5）中，如果参数x比较小，这时获取的函数值就比较大，相应的增益也会很大；反之就是增益比较小，此时神经网络不容易进入饱和状态。
BP神经网络主要是通过有监督的学习方式来对样本进行训练，神经网络通过训练好的模型，那么网络中的神经元可以通过相应的激活值，然后从输入层通过中间的隐层，最后通过输出层进行输出，此时通过输出层中的神经元来进行相应的网络响应来实现输出。然后，通过对比实际网络中的误差与期望误差进行对比，如果达不到期望误差值，此时会通过输出层到隐层，然后回到原始输入层进行修改相应的权值，依次循环上述的过程直到达到期望的误差值或者循环的最大次数才会停止。我们称这样的修改权值过程为“误差逆传播”。BP神经网络正是通过这样的误差逆传播来提高网络的学习效率和正确输入响应的能力。在整个神经网络运行的过程中主要存在两种信号：一种是误差信号，即网络中的实际输出和期望输出之间的误差值；另一种是工作信号，即在输入端进行相应的输入时，最后输出端也会有相应的输出响应信号。
另外BP神经网络还具有很强的映射能力，假设存在一组输入向量x，并有x∈Rn，那么x=（x0，x1，…，xn-1）T，此时如果网络中隐层的神经元一共有n1，这里可以用x′来表示输入向量对应隐层中的输出，那么x′=（x0′，x′1，…，xn′1-1）T，假设在输出层中神经元总数为m，且y∈Rm，y=（y0，y1，…，ym-1）T。在网络中的输入层到隐层之间的权值可以用wij来表示，相应的阈值可记为θj，隐层到输出层之间的权值可用wj′l来表示，相应的阈值可用θj′来表示。此时网络中各层相应的输出可表示如下：
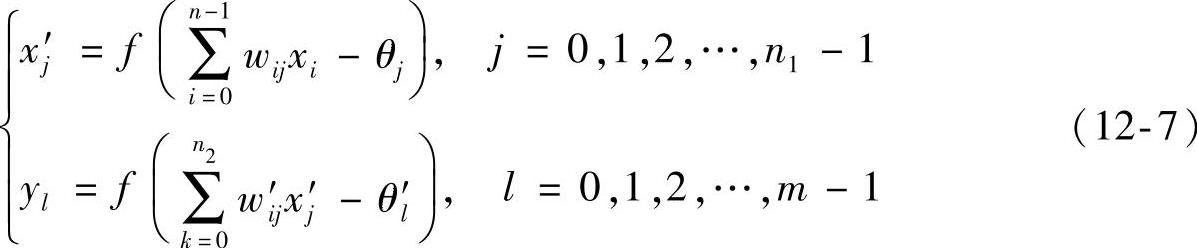
式（12-7）可以看成是n维向m维空间进行映射。