10.4 快速固定点ICA算法
快速固定点ICA算法又称为FastICA算法,是一种快速寻优的迭代算法。我们通常用负熵来度量非高斯性,基于负熵最大的FastICA算法是寻找一个使负熵最大的方向,即一个单位长度向量w,使得对应的投影y=wTz具有最大的非高斯性。非高斯性在这里是利用负熵的近似J(wTz)来度量的。基于负熵最大的FastICA算法结合了固定点迭代的优良算法特性与负熵良好的统计特性,因此是一种有效并且快速的ICA算法。
FastICA算法的推导如下:wTz的近似负熵的极大值通常在E{G(wTz)}的极值点处取得,根据拉格朗日条件,E{G(wTz)}在约束E{(wTz)2}=w2=1条件下的极值是在使下式梯度为零的点处取得:
E{zg(wTz)}+βw=0 (10-23)
式中,β=E{wT0Xg(w0TX)},是一个恒定值,其中w0是优化后的w值。下面利用牛顿法来求解式(10-23),用F表示式(10-23)左侧的部分,求得其梯度为

为了简化矩阵求逆,需要对式(10-24)中右侧的第一项进行近似。因为数据已经经过白化处理,E{zzT}=I,所以E{zzTg′(wTz)}≈E{zzT}E{g′(wTz)}=E{g′(wTz)}I,这时梯度变成了对角化的矩阵,可以简单地求逆。因而可以得到近似的牛顿迭代算法如下所示:
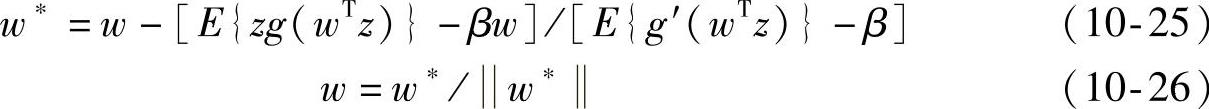
式中,w∗为w的新值;β=E{wTzg(wTz)};g(·)为非线性函数。g(·)常选用下列函数:
g1(u)=tanh(a1u) (10-27)
g2(u)=uexp(-u2/2) (10-28)
g3(u)=u3(10-29)
经过简化可以得到FastICA算法的迭代公式为
w∗=E{zg(wTz)}-E{g′(wTz)}w (10-30)
经过标准化得到w=w∗/w∗。
FastICA算法的基本步骤如下:
1)将观测数据进行中心化使其均值为0。
2)然后进行白化,得到z。
3)选择一个具有单位范数的初始化(可随机选取)向量w。
4)更新w∗=E{zg(wTz)}-E{g′(wTz)}w,函数g的定义见式(10-27)~式(10-29)。
5)标准化w,w=w∗/w∗。
6)如果尚未收敛,返回步骤4。
同理,可以推广到估计多个分量的情况,计算步骤如下:
1)对观测数据X进行中心化,使它的均值为0。
2)对数据进行白化,X→Z。
3)选择需要估计的分量的个数m,设迭代次数p←1。
4)选择一个初始权矢量(随机的)Wp。
5)令Wp=E{Zg(WpTZ)}-E{g′(WpTZ)}W,非线性函数g的选取见式(10-27)~式(10-29)。
6)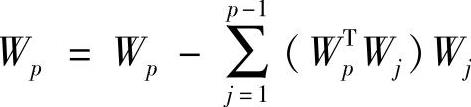 。
。
7)令Wp=Wp/Wp。
8)假如Wp不收敛,返回步骤5。
9)令p=p+1,如果p≤m,返回步骤4。
FastICA算法的收敛速度快,和梯度算法不同,无须选择步长参数,易于使用。它的性能能够通过选择适当的非线性函数g来优化,并且能够利用非线性函数g直接分离出任何非高斯分布的独立分量,不必像其他算法一样需要进行概率密度函数的估计。它与投影追踪相类似,独立分量可以被逐个估计出来,因此在只需要估计出一小部分独立分量的情况下,可以减少计算量。FastICA算法与神经网络算法一样有很多优点,它是并行的、分布式的且计算简单,内存要求很少。
