8.3.3 主成分的推导
在下面推导主成分的过程中,需要用到线性代数中的两个定理:
定理一:若A是p×p阶是对称阵,则一定可以找到正交阵U,使
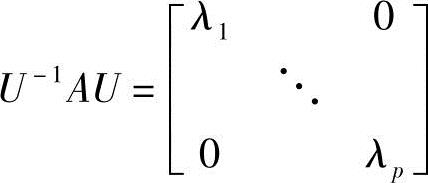
式中,λ1,λ2,…,λp是A的特征根。
定理二:若上述矩阵A的特征根所对应的单位特征向量为u1,u2,…,up,令
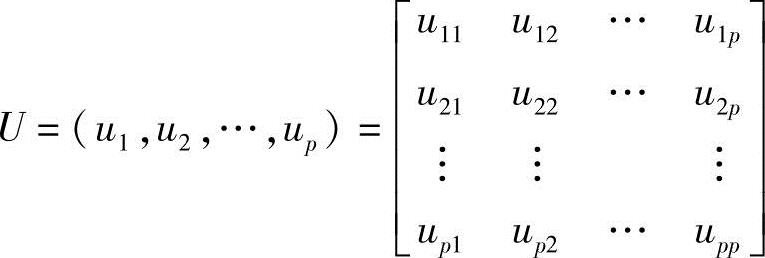
则实对称A属于不同特征根所对应的特征向量是正交的,即
uiu2=0⇒UU′=U′U=I
主成分的推导过程如下:
设F=a1X1+a2X2+…+apXp=a′X,其中a=(a1,a2,…,ap)′,X=(X1,X2,…,Xp)′,由主成分的定义可知,求取主成分也就是寻找X的线性函数a′X使相应的方差尽可能的大,即使
Var(a′X)=E(a′X-E(a′X))(a′X-E(a′X))′
=a′E(X-EX)(X-EX)′a
=a′Σa达到最大值,且a′a=1。
设协方差矩阵Σ的特征根为λ1≥λ2≥…≥λp>0,其对应的单位特征向量为u1,u2,…,up。令
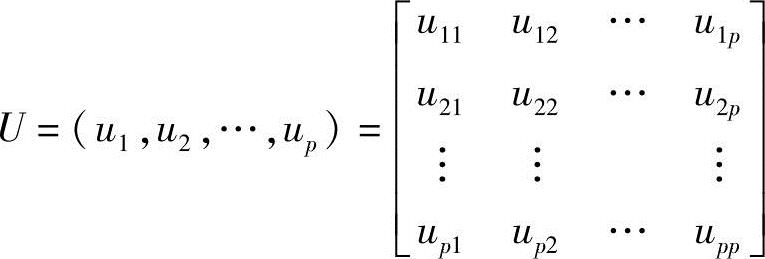
由前面的线性代数定理可知,UU′=U′U=I,且

因此
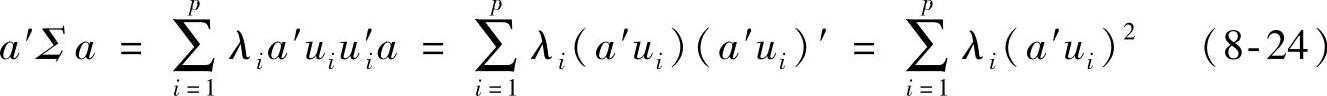
所以
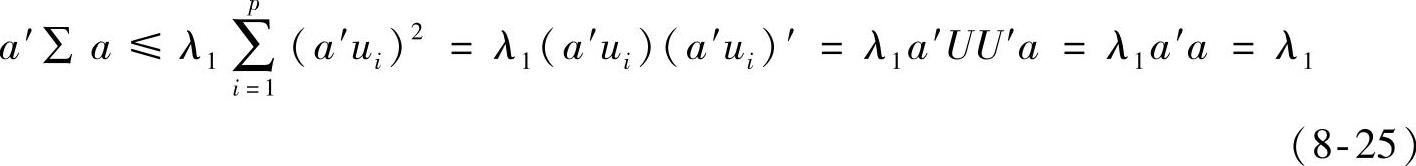
而且,当a=u1时,有
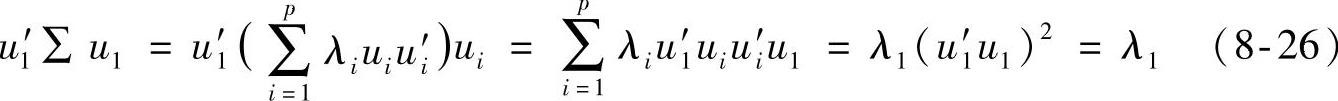
因此,a=u1使Var(a′X)=a′Σa达到最大值,且
Var(u1′X)=u1′Σu1=λ1(8-27)同理
Var(ui′X)=λi(8-28)而且
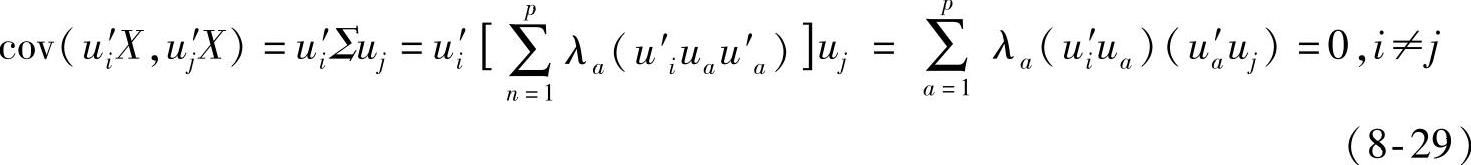
上述推导过程表明,以Σ的特征向量为系数的线性组合就是X1,X2,…,Xp的主成分,它们彼此互不相关,其方差为Σ的特征根。
由于Σ的特征根λ1≥λ2≥…≥λp>0,所以有Var(F1)≥Var(F2)≥…≥Var(Fp)>0。这就是主成分的次序按照特征根取值大小顺序排列的原因。
在解决实际问题时,一般不是取全部的p个主成分,确定新变量的个数k是一个关键问题。k越小,越能降低数据维数,便于分析,同时也能降低噪声。但是如果k过小,会导致一些有用的信息丢失,累计贡献率的大小反映了前k个主成分代替原始变量时的可靠性。贡献率越大,可靠性越大;反之,则可靠性越小。因此,根据累计贡献率的大小取前k个主成分。称第一主成分的贡献率为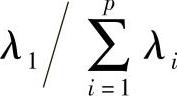 ,由于Var(F1)=λi,所以
,由于Var(F1)=λi,所以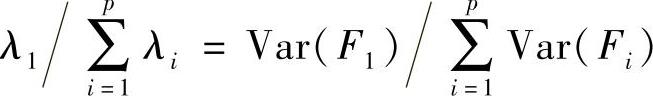 。因此第一主成分的贡献率就是第一主成分的方差占全部方差
。因此第一主成分的贡献率就是第一主成分的方差占全部方差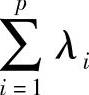 的比例。这个值越大,表明第一主成分综合X1,X2,…,Xp信息的能力越强。
的比例。这个值越大,表明第一主成分综合X1,X2,…,Xp信息的能力越强。
前两个主成分的累计贡献率定义为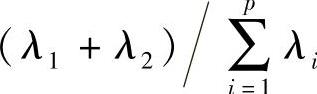 ,以此类推,前k个主成分的累计贡献率为
,以此类推,前k个主成分的累计贡献率为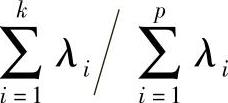 。如果前k个主成分的贡献率达到85%,就表明前k个主成分中所包含的信息和那p个主成分所包含的几乎一样多。取这k个主成分就可以取代原始的那p个主成分,于是对p个主成分的n次测量值所组成的原始数据集,就压缩为对k个主成分的n次测量值所组成的数据集,这样既减少了变量的个数,又便于对实际问题的分析和研究。
。如果前k个主成分的贡献率达到85%,就表明前k个主成分中所包含的信息和那p个主成分所包含的几乎一样多。取这k个主成分就可以取代原始的那p个主成分,于是对p个主成分的n次测量值所组成的原始数据集,就压缩为对k个主成分的n次测量值所组成的数据集,这样既减少了变量的个数,又便于对实际问题的分析和研究。
值得指出的是,当协方差矩阵Σ未知时,可用其估计值S,即样本协方差矩阵来代替。
设原始数据资料阵为
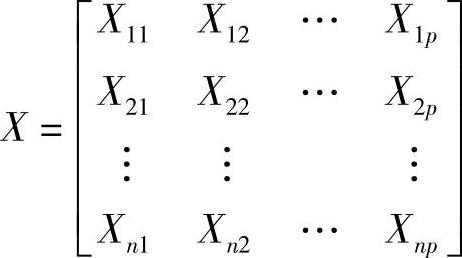
则S=(sij),其中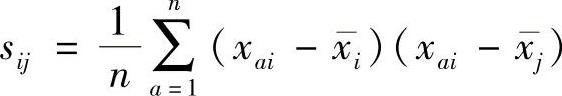 。而相关系数矩阵为
。而相关系数矩阵为
R=(γij)
式中,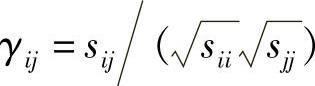 。当原始变量X1,X2,…,Xp标准化后,则
。当原始变量X1,X2,…,Xp标准化后,则

在实际应用时,指标的量纲往往不同,因此在计算之前应先消除量纲的影响,即将原始的数据标准化。这样一来S和R相同。所以一般求R的特征值和特征向量,就不妨取R=X′X,因为这时的R与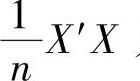 只相差一个系数。虽然X′X与
只相差一个系数。虽然X′X与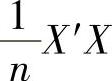 的特征根相差n倍,但是它们的特征向量不变,并不影响主成分的求取。
的特征根相差n倍,但是它们的特征向量不变,并不影响主成分的求取。
由主成分分析的定义和基本原理的讨论大体已经可以看出进行主成分分析的步骤,在此概括如下:
1)将原始观察数据组成样本矩阵X,每一行代表一维数据,每一列为一个观察样本。
2)将样本矩阵X进行标准化处理,计算其协方差矩阵Σ:
Σ=E(XX′)=E(X-EX)(X-EX)′
3)计算协方差矩阵Σ的特征值λi及相应的特征向量ui,i=1,2,…,p。
4)计算各主成分的贡献率ak和累计贡献率a(k)。
5)确定主成分的个数,构成特征空间。
通常情况下,a(k)取0.9~1之间的数值。将特征值按贡献率由大到小的顺序排列,选取前k个较大特征值对应的特征向量,构成变换矩阵U=(u1,u2,…,uk),即为特征空间。
将样本矩阵投影到这个特征空间,求出其系数向量,这就是样本矩阵X的主成分,求出融合后的特征,即Fi=UTXi,i=1,2,…,p。
