7.4 融合实验结果与分析
上述详细地介绍了利用协方差矩阵多特征融合算法的每个详细步骤公式,下面就验证此算法的可靠性和有效性,通过对它进行基于VisualC++6.0编程和具体图像数据仿真来进行试验。在本次仿真实验过程中,因为涉及的图像数据比较多,考虑到复杂度和易操作性,我们选取了坦克、越野车和直升机来作为图像目标,以下的图片都是通过识别系统外部可见光和红外传感器真实采集到的图像信息进行特征融合处理,对采集到的源图片进行预处理去噪增强,通过训练和建模建立图像目标的特征数据库,在实验中,考虑到数据非常大,暂时每组200张图片,其中可见光和红外各100张,尺寸均为128像素×128像素。在图7-3中显示的就是数据库中的一些图片,其中上面是可见光图片,下面为红外图片。
根据上述对可见光和红外图像特征提取可分为八个维度对目标特征进行提取。通过在VisualC++6.0上进行编程处理得到了相应的特征值,见表7-1,它是图7-3a的部分特征值数据。
通过对图7-4a、b、c、d进行不同方向的旋转、侧翻和缩放的图像协方差特征值测试。然后求得它们的特征协方差曲线图如图7-5所示,根据图中曲线的变化可以看出,对于图像中目标的旋转、侧翻和适度缩放对其特征值的影响非常小,所以能得出特征协方差矩阵具备非常强的旋转不变性、尺度不变性和适应鲁棒性的结论。

图7-3 融合的部分类别图像
表7-1 图7-3a中部分图像的特征值
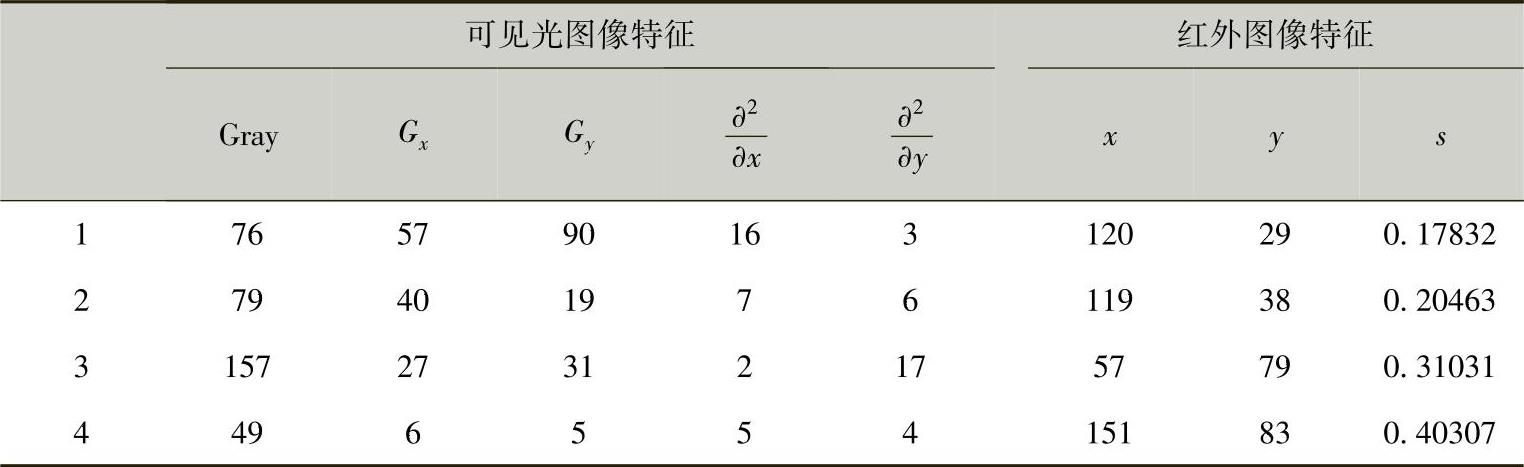

图7-4 测试图像
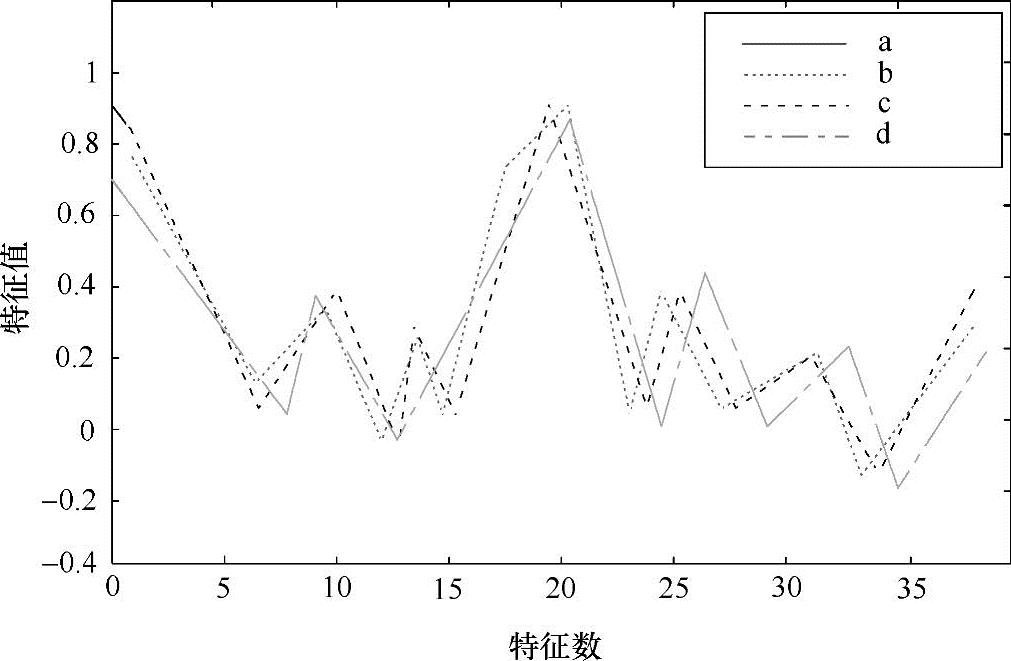
图7-5 协方差矩阵特征值曲线
根据上面实验仿真数据可以总结出利用协方差矩阵对目标特征信息融合的优点如下:在公式计算和推导中我们能够清楚地知道,协方差矩阵的大小只和我们提取目标特征向量的维数有关系,如果我们想要再对目标特征进行更多的特征添加也只需要加上相应的维数就行,从而有效地降低了相应的计算量;在后面对目标图像进行旋转、侧翻和缩放测试中,协方差矩阵获得特征值基本是不变或者相差非常小,从而从实验到理论验证了协方差矩阵具备非常好的旋转不变性、尺度不变性和鲁棒性。
