10.3.1  非高斯性

10.3.1 非高斯性

非高斯性在ICA模型的估计中扮演着极为重要的角色，是实现ICA估计的一个基础，独立成分可以通过寻找数据具有最大非高斯性的方向而得到，而非高斯性可以利用熵或者累积量（如峭度）来度量。实际在自然界中真正满足高斯分布的信号很少，所以ICA方法的研究有非常重要的意义，并且应用前景广阔。ICA以统计独立性为基本原则，非高斯性极大是度量ICA独立性的重要方法，它的思想来源于中心极限定理。

定理10.1（中心极限定理）：设随机变量x₁，x₂，…，x_n相互独立，它们的期望和方差见式（10-10）所示：

E{x_k}=μ_kD{x_k}=σ²≠0 k=1，2，…，n（10-10）记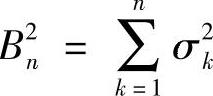，若存在正数δ，使得当n→∞时，令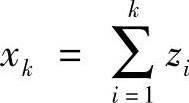为某独立同分布随机变量{z_i}的部分和序列。因为当k→∞时，x_k可能无界地增长，进而考虑标准化的变量，其公式见式（10-11）所示：

可以说明，当k→∞时，y_k的分布收敛于具有零均值和单位方差的某个高斯分布。

中心极限定理可以推广到具有共同均值m_z和协方差矩阵C_z的随机向量z_i的情形。随机向量序列见式（10-12）所示：

它的极限分布是一个具有零均值和协方差为C_z的多元高斯分布。

由中心极限定理可知，在一定条件下，相互独立的各个随机变量之和的分布趋向于高斯分布，两个独立随机变量之和形成的分布比两个原始的随机变量中的任意一个更接近于高斯分布。也就是说，最大化信号的非高斯性和独立性是一致的，这也就是所谓的“非高斯性就是独立的”。

为了在ICA估计中使用非高斯性，我们必须对一个随机变量（如y）的非高斯性定义一个度量指标。下面将介绍两个度量信号非高斯性的重要指标：峭度和负熵。

（1）峭度

随机变量的四阶累计量又叫作峭度，是经典的非高斯性度量指标。

在零均值的情况下，y的峭度kurt（y）可定义为

kurt（y）=E{y⁴}-3（E{y²}）2（10-13）

也可以用规范化的峭度，其定义为

对于白化的数据，E{y²}=1，因此峭度的两个定义都归结为

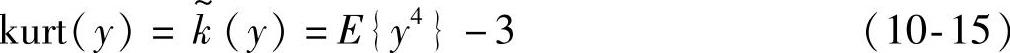
这意味着对于白化数据，四阶矩E{y⁴}可以替代峭度来刻画y的分布，这也说明，峭度实际上就是四阶矩的一种规范形式。高斯变量的峭度为零，对于高斯分布的变量y，其四阶矩等于3（E{y²}）2。

在ICA及其相关领域，峭度的绝对值或2次方已被广泛地用作非高斯性的度量，这主要是因为其无论从理论研究还是计算上都非常简单。从计算角度，在样本方差保持不变的情况下，峭度可以简单地用样本数据的四阶矩来估计。由于在两个随机变量相互独立的情况下，峭度具有以下两种线性特点，因此理论分析也相应得到简化。设y₁和y₂是两个相互独立的随机变量，则式（10-16）和式（10-17）两式恒成立：

kurt（y₁+y₂）=kurt（y₁）+（y₂）（10-16）

kurt（αy₁）=α⁴kurt（y₁）（10-17）式中，α为常数。

（2）负熵

熵是信息论中的基本概念，用来衡量随机变量出现的期望值。对于一个离散取值的随机变量X，它的熵H定义为

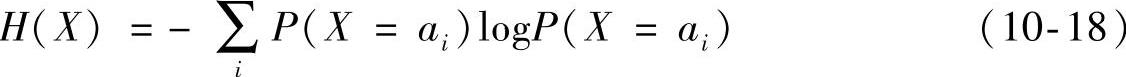
式中，a_i为X的可能取值。

取不同的对数基底，将得到熵的不同单位。通常情况下取2作为基底，这时的单位是bit。

负熵也是度量非高斯性的一个重要指标，负熵J定义为

J（x）=H（x_gauss）-H（x）（10-19）式中，x_gauss为高斯随机向量。

它与x具有相同的协方差矩阵。它的熵可以由式（10-20）计算得到，即

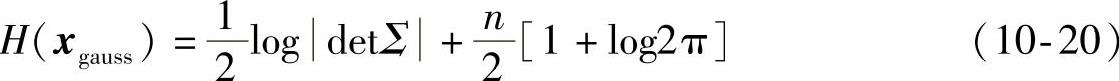
式中，n为x的维数。

负熵总是非负的，它在可逆线性变换下是不变的，这是因为，对y=Mx，有E{yy^T}=MΣM^T，负熵可以用式（10-21）计算：

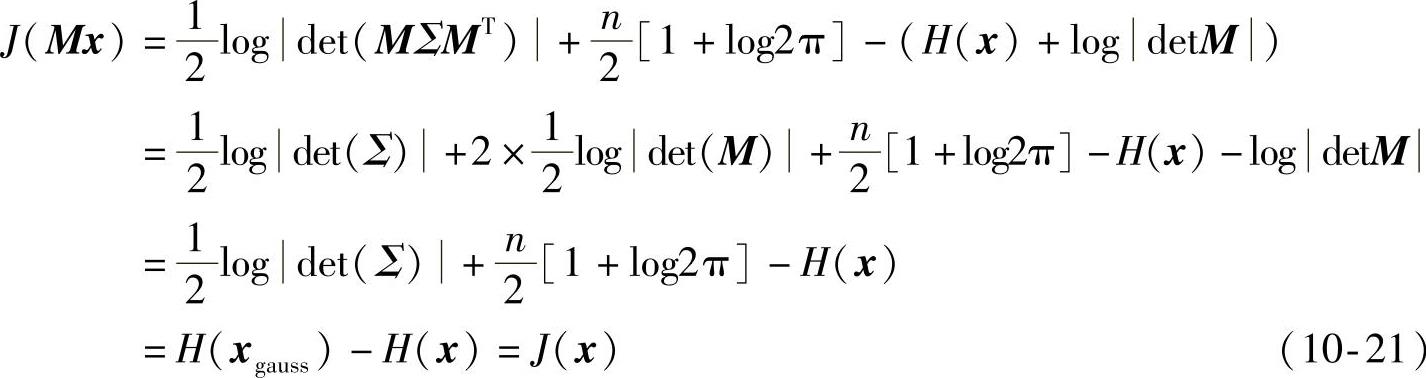
负熵是尺度不变的，也就是说，把一个随机变量乘以某个常数，不会改变它的负熵。