5.2.1  划分聚类算法

划分聚类算法采用目标函数最小化策略把一个确定的N个数据对象的数据集分成k个组，并且该算法使得每一组中的对象相似度相当高，而不同组的对象相似度比较低，由此可知相似度的定义是划分聚类算法的关键环节。该算法的目标函数一般定义为式（5-5），其中x_i表示对象空间中一个数据对象，且x_i是第i类的均值，J为集合A中全部对象与对应的聚类中心的均方差之和。最常用的划分聚类算法包含k-means算法和k-medoids算法。

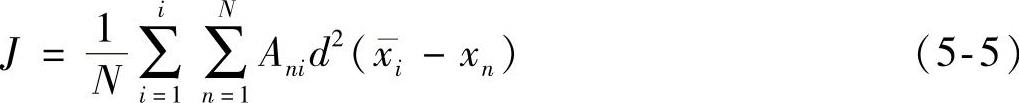
1.k-means算法

k-means算法的原理是将恒定的N个数据目标的数据集分成事先给定的数目为k的簇，首先随机选择k个对象作为初始的k个聚类中心C=（C₁，C₂，…，C_k），接着通过算出其余的所有样本到各自聚类中心的距离，把该样本划分到距离它很近的类中，之后再使用平均值的方法计算调整后的新类的聚类中心，重复上述步骤直到计算出的两次类中心保持不变时，标志着数据集中的样本分类结束且聚类平均误差准则函数F处于收敛状态，聚类平均误差准则函数F的表达式见式（5-6），其中q为数据集的数据对象，m_i是第i类聚类中心C_i的平均值，F代表数据集中全部数据对象的平方误差的总和。

k-means算法虽然容易实现，但是该算法也具有一些缺陷：k-means算法当选用不一样的初始值时，能够得到不相同的聚类结果，因此该算法对初始聚类中心的依赖性较大；k-means算法对独立点及噪声点反应较为敏锐，严重时会导致聚类中心的偏离；k-means算法需要预先掌握的知识来求出待生成的簇的数目。

2.k-medoids算法

k-medoids算法的处理过程如下：先随意选出k个对象作为初始的k个聚类的代表点，接着算出其余的样本到其最靠近聚类中心的对象的距离，把该样本归类到离它最近的聚类中，并依据某代价函数估算目标与代表点间的相异度平均值，若对象与代表点相似则替换代表点，反复进行上述过程直到不再有对象替换代表点为止。k-medoids算法包括PAM算法、CLARANS算法以及CLARA算法。当数据集和簇的数目较大时，PAM算法的性能就会变得很差；CLARANS算法不能辨认套嵌或其余繁杂形状的聚类形状，而且该算法具有运算效率低、没有处理高维数据的能力以及不能准确找到局部极小点产生错误的聚类结果的缺陷；CLARA算法的聚类结果与抽样的样本大小有关，当抽样的样本发生偏差时，CLARA算法的性能就会变差而不能得到良好的聚类结果。