13.2.3  最优超平面

13.2.3 最优超平面

假设存在一个线性可分的训练集S={（x_j，y_j）}_j′=1，线性可分是指训练集中不同类别的样本点能够被一个线性超平面正确分开。我们可以将这个分类超平面用公式描述为

w·x+b=0（13-16）

式中，w是超平面的法线方向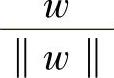，为单位法线方向，‖w‖为w的模，wx为w与x的内积，这里b∈R，w∈Rⁿ，x∈Rⁿ。

分类结果可以表示为

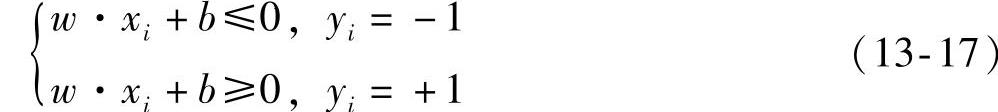
我们可以假设空间：

f（w，b）=sgn（w·x+b）（13-18）

对（w，b）进行如下约束：

minw·x_i+b=1（13-19）

我们的目的是为了完全正确地进行分类，显然能够满足分类目的的分类超平面未必只有一个。如图13-6所示，该分类超平面也可以完全正确地对两类样本进行正确的分类。尽管能够正确分类的超平面不唯一，但是最优分类超平面是唯一的。所谓最优分类超平面是指能够满足距离该超平面最近的两类区域边界处的训练点之间的距离最大（见图13-6），我们称间隔为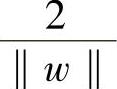的分类超平面为最优分类超平面。支持向量就是指这些距离最优超平面最近的处于类别区域边界上的样本点，正是利用这些支持向量才唯一地确定了最优分类超平面。

图13-6和图13-7对比描述了最优分类超平面与普通分类超平面的结构比较，通过两幅图形的对比可以很直观地看出两类分类超平面的差异。图13-6中H为最优分类超平面，H₁和H₂分别为两个类别区域的边界超平面，两者经过各自类别区域中位于边界上的样本点并与H平行，称H₁和H₂之间的距离为分类间隔。这里的最优是指分类间隔能够达到最大值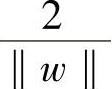。由约束条件式（13-19）可知：

H：w·x+b=0

H₁：w·x_i+b≥1，y_i=+1（13-20）

H₂：w·x_i+b≤-1，y_i=-1

两种情况可以简写成：

y_i（w·x_i+b）≥1，i=1，2，…，l（13-21）

式中，H₁和H₂到H的距离为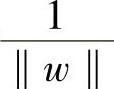，分类间隔为。

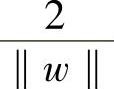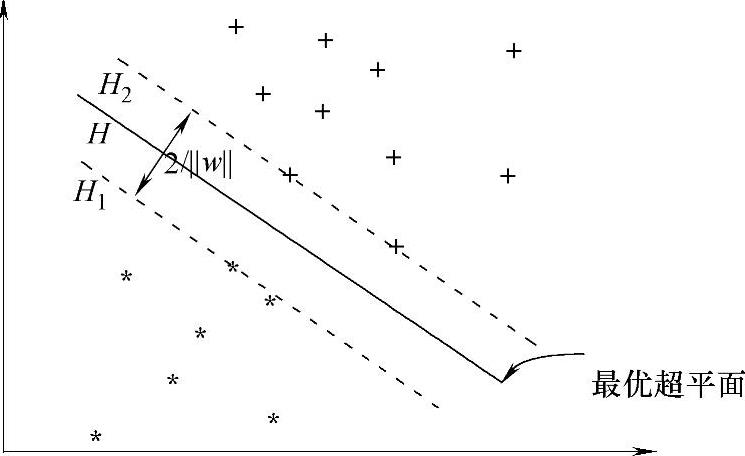
图13-6 最优分类超平面

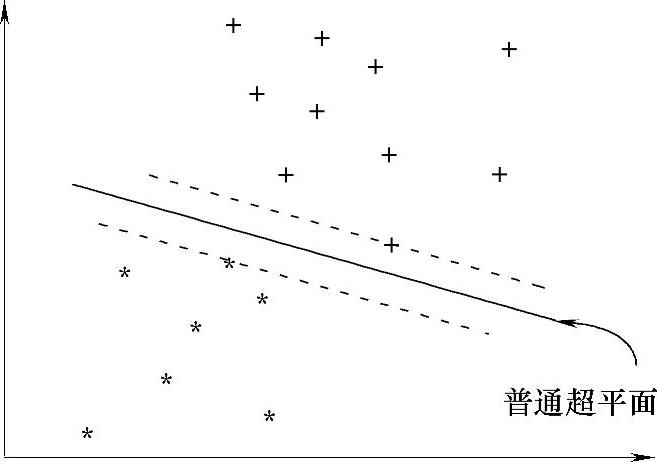
图13-7 普通分类超平面