13.1.2  模糊集

模糊数学是描述模糊现象的数学。而模糊集是模糊数学的理论基础。对于我们熟悉的普通集论要求：论域U中每个元u，对于子集A⊆U来说，u与A只存在u∈A或者u∉A两种关系，不会出现模棱两可的现象。因而，子集A可用0和1两个数字来刻画。设论域U为自然数集，那么上述关系可以用特征函数法表示为

C_A∶U→{0，1}

u→C_A（u）（13-1）

式中，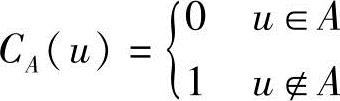

可见，给定了论域U上的一个子集，就等于给定了特征函数，反之亦然。因此，一个特征函数对应着集合里的一个值。

传统的数学理论中特征函数的取值范围是{0，1}，而L.A.Zadeh教授则将这个范围进行了拓展，将取值范围由原来确定的两个数值拓展到了一个闭区间[0，1]。这也是模糊集概念的来源。

设在论域U上给定了一个映射：

A∶U→[0，1]

u|→A（u）（13-2）则称A为论域U上的模糊集（FuzzySet），A（u）称为A的隶属度函数，用来求得u对A的隶属度。

隶属度可以理解为是用来表示一个样本与模糊集合之间相关性程度的值。当A（u）=1时，表示样本u完全属于模糊集合A；反之，当A（u）=0时，表示样本u完全不属于模糊集合A。A（u）的值与样本u属于模糊集合A的程度成正比。