7.2.3  特征协方差

假如通过外部传感器获得的图像I为二维数字图像，此时可以假设目标在该图像区域R中的大小为M×N，那么接下来在区域R内特征点就能够用特征向量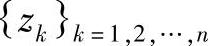来表示，其中n代表在区域R中的特征点数，在特征向量中，它的变量种类信息很多，不仅能够用图像中像素的亮度、纹理、梯度，而且还能用一些滤波器对图像中像素的响应值来表示。根据上述假设的目标区域R，它的协方差矩阵Q_R能够通过使用一个大小为d×d矩阵对其定义：

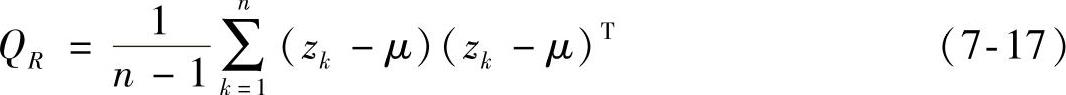
式中，。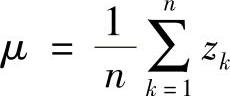

利用协方差矩阵的好处就是它不仅可以充分地将图像区域中的有效目标特征信息进行融合，其他的还能将一些图像中的表象特征信息包含在其中，比如图像直方图的特性。在上述过程中我们能够知道协方差矩阵Q_R其实是一个大小为d×d的实对称矩阵，在几何原理中也称为正定矩阵，我们知道正定矩阵的特点是在它的两条对角线上的分量都是互相独立的图像特征量，在矩阵其他区域的值就是代表与其具有相关性关系的特征量，协方差矩阵Q_R之前设它的大小为d×d，其中它的大小只跟我们所获取的特征向量的维数d有关系，其他的如目标区域都跟它没有关系，这点是非常重要的。通过对协方差矩阵中多特征值进行平均值运算，它们中的一些特征噪声就会被滤除，从而使得协方差矩阵具有很好的鲁棒性。比如在传感器对目标进行图像信息采集时，由于受到外界光照强度的干扰，会使得获取的目标图像颜色信息发生变化，但是这不会影响到协方差特征值，所以目标采集数据不会受很大的影响。