13.3.2  第二种模糊支持向量机

13.3.2 第二种模糊支持向量机

第二种模糊支持向量机的概念是由Chun-FuLin、Sheng-DeWang、Yi-HungLiu和Han-PangHuang等人于2002年提出。在传统的支持向量机的优化问题中，为了减少对样本点错分的情况，提出了惩罚参数的概念。惩罚参数C的具体作用就是当发现分类器出现错分的情况时给予一个惩罚，惩罚力度由惩罚参数C来控制，而且惩罚力度正比于惩罚参数的值。但是不管C的值是多少，一旦C的值确定了，那么在支持向量机的整个训练过程中这个值都不再改变，所以，传统的支持向量机对所有的训练样本点其实是同等对待的，没有任何区别。这种情况导致了支持向量机对一些特别情形的过分敏感，而且这种敏感是我们所不希望的。例如我们前面讲到的距离类别中心位置很远的孤立的样本点或者是噪声，这样就会出现过学习现象，使得分类器泛化能力下降。

既然已经找到了问题出现的原因，那么要解决该问题就只需要找到正确的解决方法就可以了。既然噪声点和距离类别中心较远的孤立样本点对于分类造成了不利的影响，那么我们只要对这些特殊的样本点采取一些措施来减少它们对分类的贡献度，应该就能得到更为理想的分类超平面了。因此我们针对样本点的性质分别赋予不同的隶属度，原则就是，贡献越大，隶属度越高，反之隶属度就低。采取这种措施就可以尽量减小噪声点和孤立样本点的隶属度数值，从而有效地减少噪声和孤立点对训练过程中分类性能造成的不利影响。

针对两分类问题，首先对训练样本集定义一个隶属度函数。之后根据隶属度函数，将所有的训练样本进行模糊化处理，得到每个训练样本x_i的隶属度s_i。最后将训练样本集改写为模糊训练样本集，将隶属度信息添加到样本点数据中。

假设模糊训练集合为

S={（x₁，y₁，s₁），（x₂，y₂，s2），…，（x_l，y_l，s_l）}（13-28）式中，x_i∈Rⁿ，y_i∈{-1，+1}，s_i∈（0，1]。

s_i表示训练样本x_i与其对应的输出y_i之间的隶属度数值。隶属度的值表示训练样本x_i对分类结果的重要程度，而参数ξ_i为支持向量机的松弛变量，表示容错程度。因此，s_iξ_i可以用来衡量对于分类重要性不同的变量的容错程度。

对于前面所描述的训练集，通过解如下的优化问题可以得到我们所期望的最优分类超平面：

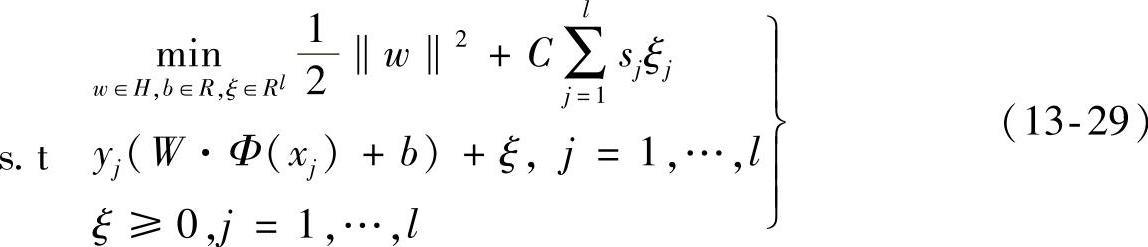
式中，C>0是惩罚参数，s_j是模糊隶属度，ξ=（ξ₁，…，ξ_i）T。

求解式（13-29）二次规划的对偶规划，构造拉格朗日函数：

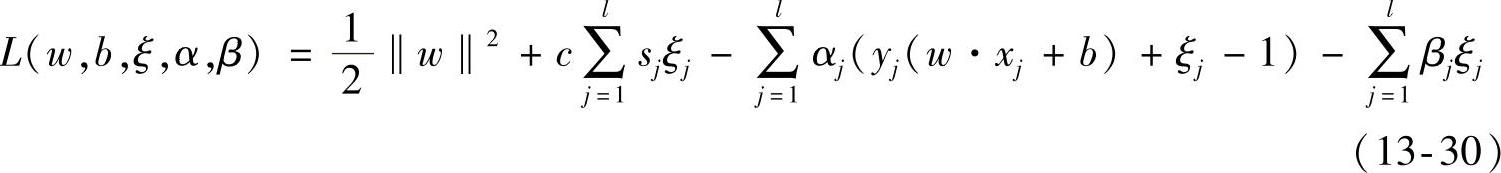
式中，α=（α₁，α₂，…，α_l）T，β=（β₁，β₂，…，β_l）T，α_j≥0，β_j≥0（j=1，2，…，l）。

根据对偶的定义，对式（13-30）关于w、b和ξ_j求极小值，求偏导如下：

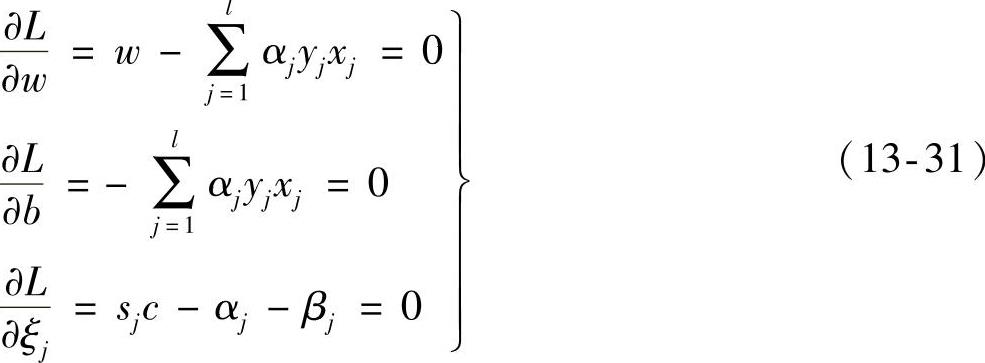
将式（13-31）代入式（13-30）中，得二次规划的对偶规划为

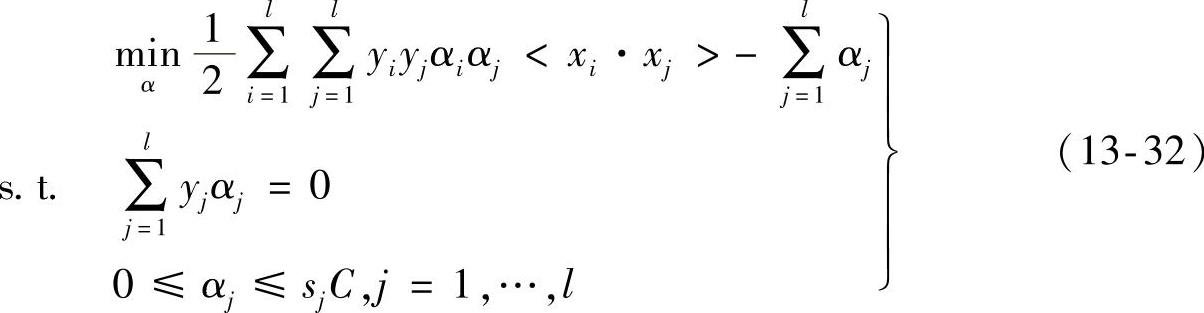
因此，通过前面的推导我们得到了最优超平面问题的对偶形式，根据对偶的性质，通过求得对偶形式的最优解也就得到了我们所期望的最优分类超平面。可以看出式（13-32）为一个凸二次规划问题，所以可以解得最优解α∗=（α₁∗，…，α_l∗）T，据此我们得到模糊最优分类函数公式如下所示：

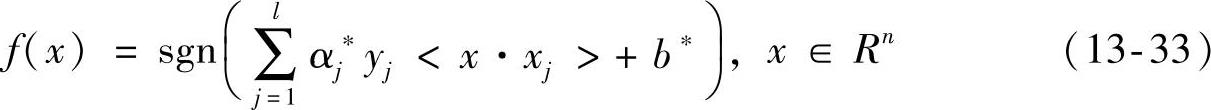
若存在α∗的正分量α_j∗使得α_j∗∈（0，x_jC），则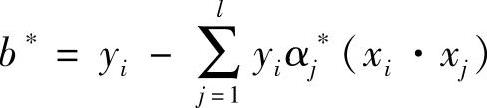，其中下标i∈{i0<α_i∗<s_jC}。若α_j∗>s_jC，为错分的样本点。这种模糊支持向量机与传统的支持向量机最大的不同在于，由于s_j的出现，使得模糊支持向量机中α_j∗所对应的支持向量与传统的支持向量机中对应的支持向量有可能发生变化，也就是前后两者所对应的不再是同一类支持向量。

对于非线性问题，我们引入核函数K（x_i，x_j），那么分类问题可用如下的二次规划表示：

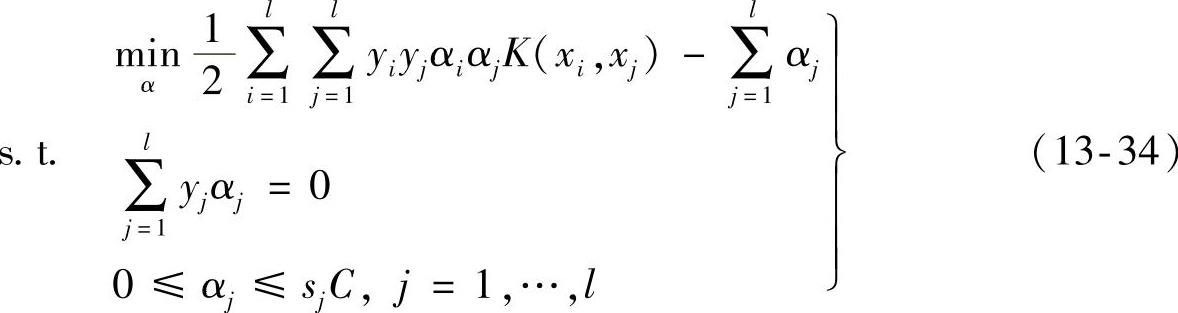
通过式（13-34）可以看出，这是一个凸二次规划问题，对其求解可以得到α∗=（α₁∗，…，α_l∗）T为最优解，据此我们所求的模糊最优分类函数可以表达为如下形式：

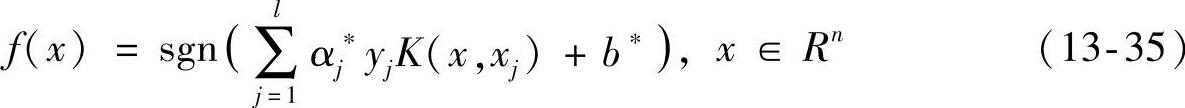
式中，。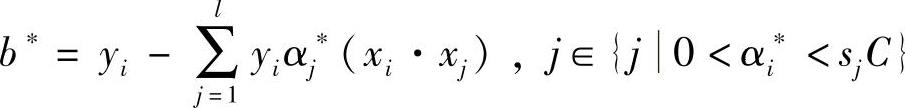

对于式（13-35）中α_j值，只有当样本点为支持向量时才会有非零值的可能，其他情况均为零值。因此，只有支持向量才会使用式（13-35）进行求和。

综上所述，可以得出模糊支持向量机的基本思想是，通过引入模糊数学的理论构造隶属度函数，通过计算各样本点的隶属度来控制惩罚系数的大小，从而减少噪声和孤立点对分类的贡献度。采取这种措施就可以尽量减小噪声点和孤立样本点的隶属度数值，从而有效地减少噪声和孤立点对训练过程中分类性能造成的不利影响。