11.3  典型相关变量和相关系数的求解步骤

11.3 典型相关变量和相关系数的求解步骤

1.计算原始数据的协方差矩阵

设有两组变量，X代表第一组的ρ个变量，Y代表第二组的q个变量，不妨假设p≤q，令

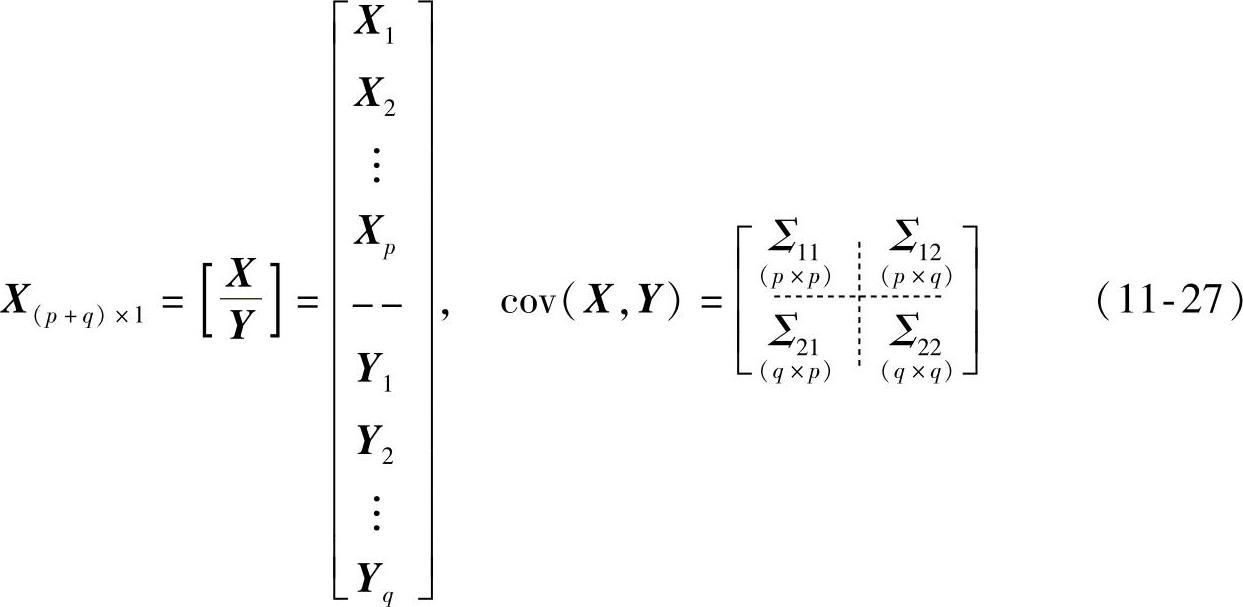
式中，Σ₁₁=cov（X）；Σ₂₂=cov（Y）；Σ₁₂=cov（X，Y）=Σ₂′₁。Σ₁₁为第一组变量的协方差矩阵，Σ₂₂为第二组变量的协方差矩阵，Σ₁₂和Σ₂₁为两组变量之间的协方差矩阵，并且有Σ₂₁=Σ′₁₂。

2.计算两个矩阵A和B

A=Σ₁^-11Σ₁₂Σ₂^-21Σ₂₁（11-28）

B=Σ₂^-21Σ₂₁Σ₁^-11Σ₁₂（11-29）式中，A为p×p阶矩阵；B为q×q阶矩阵。

3.计算A和B的特征向量和特征根

λ²₁≥λ²₂≥…≥λ²_r为矩阵A和B的非零特征根，a₁，a₂，…，a_r为A对应于λ²₁，λ²₂，…，λ²_r的特征向量，b₁，b₂，…，b_r为B对应于λ²₁，λ²₂，…，λ²_r的特征向量，则最大特征根λ²₁对应的特征向量a₁=（a₁₁，a₁₂，…，a_1p）′和b₁=（b₁₁，b12，…，b1p）′就是所求的第一对典型变量的系数向量，第一对典型相关变量如下所示：

U₁=a′₁X=a₁₁X₁+a₁₂X₂+…+a_1pX_p（11-30）

V₁=b′₁Y=b₁₁Y₁+b₁₂Y₂+…+b_1qY_q（11-31）

依次还可以求出r个典型相关系数和r对典型相关变量。