3.3.2 高通滤波
高通滤波的原理是衰减甚至截断大部分的低频成分,保留高频成分,即通高频、阻低频。高通滤波的实质是某一邻域内像素灰度值的平均值被每一个像素灰度值减去,若这个像素是目标像素,则它的值与邻域内像素卷积后的值相差很远,且此差值也极大;反之,若这个像素是非目标像素,因此它的值与邻域中的像素卷积的值很相似,且此差值也极小,因而可以滤掉每个像素中背景噪声的平均值。高通滤波的原理框图如图3-6所示。其中,f(x,y)是原始图像,F(u,v)是经过傅里叶转换后的图像,G(u,v)是高通滤波后的图像,且滤波后的图像G(u,v)要经过高通滤波的传递函数H(u,v)获得,最后经过傅里叶逆变换而获得去噪后的图像g(u,v)。
若高通滤波的脉冲响应函数为h(x,y),输入的图像信号为f(x,y),则输出的滤波后的图像信号为g(x,y),且输出的滤波后的图像信号g(x,y)的表达式见式(3-18);其频域表式见式(3-19),其中F(u,v)是输入的图像信号f(x,y)的傅里叶变换,H(u,v)为高通滤波的脉冲响应函数h(x,y)的傅里叶变换,G(u,v)为输出的滤波后的图像信号g(x,y)的傅里叶变换。因此,整个高通滤波过程的表达式见式(3-20),其中F表示傅里叶变换,F-1表示傅里叶逆变换。

图3-6 高通滤波原理框图
g(x,y)=h(x,y)∗f(x,y)(3-18)
G(u,v)=H(u,v)F(u,v)(3-19)
g(x,y)=F-1{F[f(x,y)]H(u,v)}(3-20)
对于高通滤波的整个过程,最关键的就是选取适当的脉冲响应函数h(x,y),利用h(x,y)可以使f(x,y)中的低频分量衰减,保留高频分量,起到高通滤波的作用。对于离散的多源图像的数字图像,高通滤波的脉冲响应函数通常情况下选用卷积模板,表示为矩阵H。关于模板H,它的中心像素权值越小,信号就越不容易通过;反之,其中心像素权值越大,信号越容易通过,且权值周围部分全为1,因此,高通滤波保留了图像中信号强度很高的微小目标和独立噪声点。常用的一些高通模板有h1、h2、h3、h4等,如图3-7所示。由这些模板演变出许多不同形式的高通滤波模板,它们的尺寸也不尽相同,因此滤波效果也不相同。
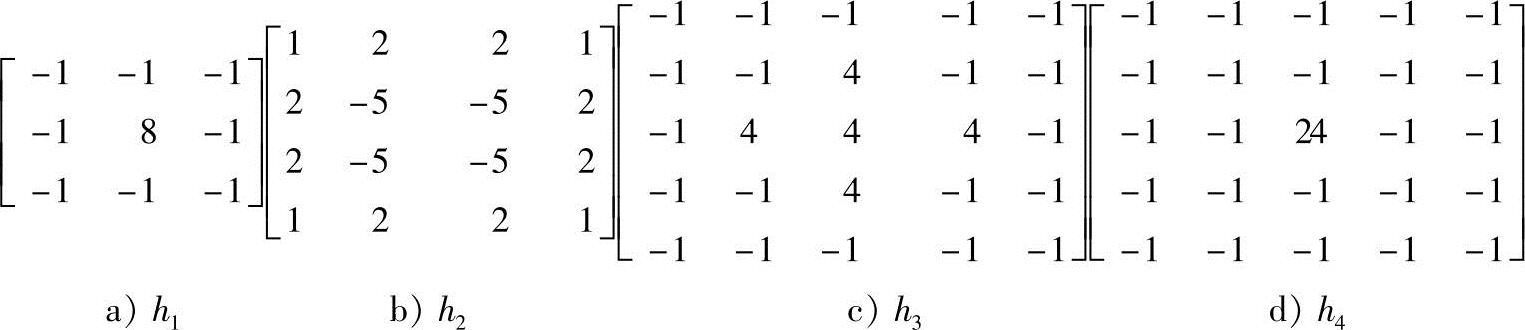
图3-7 常用的几种高通滤波模板
高通滤波方法一般情况下由输入图像与经过低通滤波后的图像的差值取得,它的一维表达式见式(3-21),其中f(n)是一维输入信号,l(n)是低通滤波的输出信号,g(n)是滤波输出图像的一维输出信号,M是低通滤波所使用的点数。l(n)的描述见式(3-22)。高通滤波的二维表达式见式(3-23),其中,f(i,j)是输入图像的信号,l(i,j)是低通滤波的输出信号,g(i,j)是滤波输出图像的二维输出信号,M是低通滤波半径,s(i,j,m)是输入图像的信号求和运算。l(i,j)的描述见式(3-24)。s(i,j,m)的描述见式(3-25)。
g(n)=f(n)-l(n)(3-21)
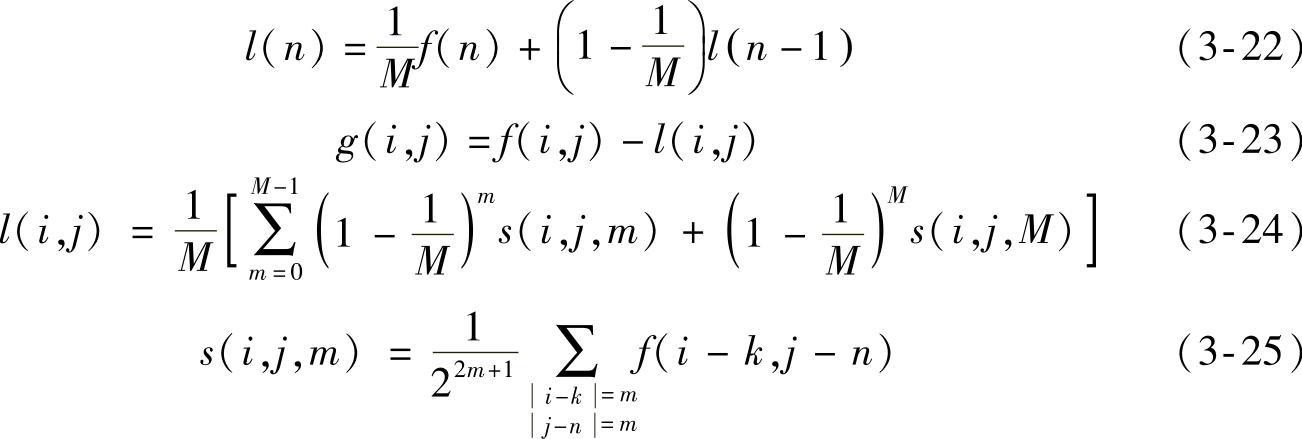
常用的高通滤波包含:理想高通滤波、指数高通滤波和巴特沃兹高通滤波。其中理想高通滤波的描述见式(3-26),指数高通滤波的描述见式(3-27),巴特沃兹高通滤波的描述见式(3-28)。其中,D0代表原点与截止频率之间的距离,D(u,v)代表点(u,v)与原点间的距离,且D(u,v)的描述见式(3-29),n代表控制传递函数H(u,v)从原点开始计算的增长率。
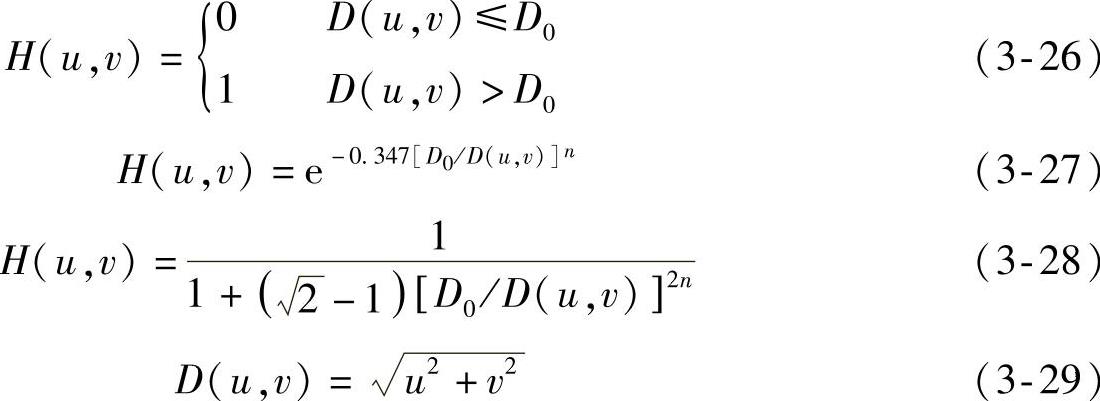
以上几种高通滤波方法均可以使图像的部分边缘变得更加清晰,而使物体在背景中更为突出。其中指数高通滤波由于具有较快的增长率,因而相对于其他方法来说更能保留图像的高频分量而起到对图像中的物体勾边的作用。但是,高通滤波虽然能去除背景,但对系统自身噪声(例如点噪声等)却无法滤除,而且在处理图像时,运算复杂,运算量极大,也不利于硬件实现,因此,高通滤波对多源图像的梯度图像的滤波效果并不是最佳的。
