6.1.3 共生矩阵
纹理反映的是图像的空间分布、灰度统计和结构信息。它是由一定大小和形状的像素集合组成的,是所有图像都具有的特性。纹理特征提取是指通过检测算法,检测出纹理基元并建立纹理模型,最终用特征量来描述。灰度共生矩阵是典型的纹理特征提取方法。它由两个位置像素的联合概率密度来定义,反映像素亮度特性及其像素之间位置关系。
共生矩阵表示像素空间的关系和依赖程度。设灰度共生矩阵中某一元素(i,j)的灰度值为i,另一个元素的灰度值为j,它们之间的距离为d,方向为θ,那么共生矩阵的值就是满足以上条件像素的个数。实际中,θ一般选为0°、45°、90°、135°。图像的灰度级一般为256,实际计算中远小于它。因为若矩阵维数过大,窗口较小,那么共生矩阵表示纹理的效果不好。若窗口较大,维数小,这样大大增加计算量,降低了实时性。所以在计算时,首先需要降低维数或减小灰度级。
设数字图像f(x,y)的大小为M×N,灰度级为Ng,则灰度共生矩阵为
P(i,j)=#{(x1,y1),(x2,y2)∈M×Nf(x1,y1)=i,f(x2,y2)=j} (6-59)式中,#(x)表示集合x中的元素个数,显然P为Ng×Ng的矩阵,若(x1,y1)与(x2,y2)间距离为d,并与横轴的夹角为θ,则可得任何间距和角度的共生矩阵P(i,j,d,θ)。图6-4为四个不同方向上的共生矩阵示意图。
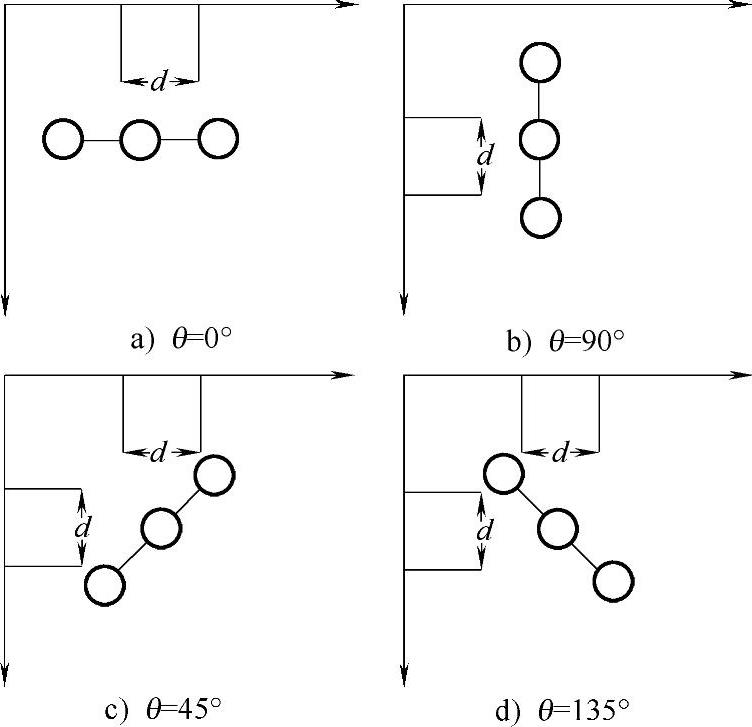
图6-4 四个不同方向上的共生矩阵示意图
纹理特征提取是以灰度级的空间相关矩阵为基础,这是因为灰度共生矩阵表示了图像中相距(Δx,Δy)的两个像素同时出现的联合频率分布。若图像灰度级为N,那么共生矩阵为N×N矩阵,可表示为M(h,k),其中位于(h,k)的元素M的值表示两个灰度分别为h和k、相距为(Δx,Δy)的像素对的出现次数。
为了使共生矩阵能更直观描述纹理,用一些统计参数来表述纹理状况,常用的有:
(1)角二阶矩

角二阶矩是图像灰度分布均匀性的度量。当共生矩阵中的元素分布比较集中于主对角线时,说明从局部区域观察图像的灰度分布是均匀的,从式(6-60)可知,它是共生矩阵中所有像素值的平方和,也可称为能量。从整个图像来看,若角二阶矩f1越大,则纹理较粗,能量越多;反之亦然。
(2)惯性矩
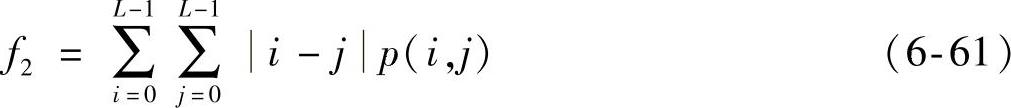
若纹理较粗,p(i,j)的值主要集中在主对角线的附近,这时i-j的值比较小,因此惯性矩也小;而纹理较细,p(i,j)数值的分布较均匀,惯性矩比较大。
(3)对比度
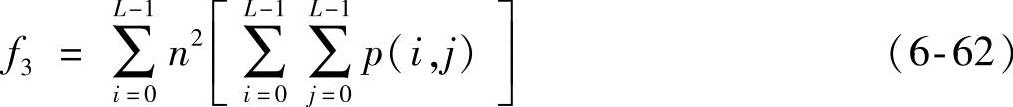
式中,i-j=n。
图像的对比度可以理解为图像的清晰度,即纹理的清晰程度。图像中纹理的沟纹越深,则其对比度f3越大,图像越清晰。反之,对比度小,则沟纹浅,效果也较模糊。
(4)相关
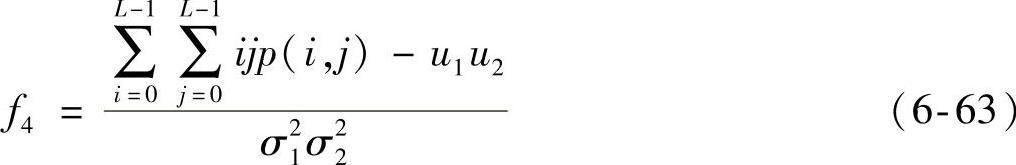
式中,
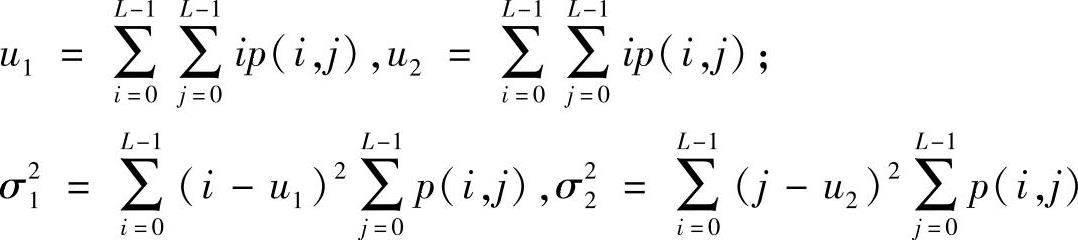
相关是用来衡量灰度共生矩阵的元素在行的方向或列的方向的相似程度。例如,某图像具有水平方向的纹理,则图像在θ=0°的灰度共生矩阵的相关值往往大于θ=45°、θ=135°或θ=90°的灰度共生矩阵的相关值。相关值的大小反映的是局部灰度的相关性。若矩阵中元素的值均匀相等,相关值就大;若矩阵中元素值相差很大,则相关值较小。
(5)熵
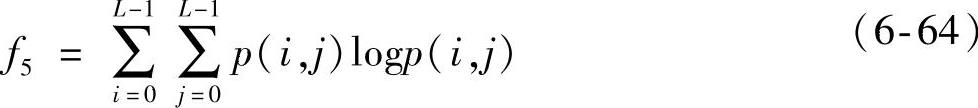
熵值是对图像中信息量的度量,纹理属于图像信息。若图像没有纹理,则熵值几乎为零。如果图像有很多细纹理,并且p(i,j)的数值比较接近,那么该图像熵值将达到最大。反之亦然。
(6)方差
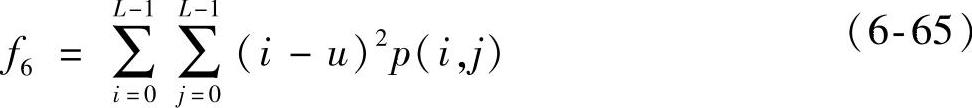
式中,u为p(i,j)的均值。
(7)和方差
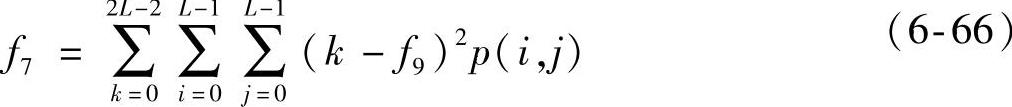
方差、和方差反映了纹理的周期大小,它们的值越大,表明纹理的周期越大。
(8)逆差矩
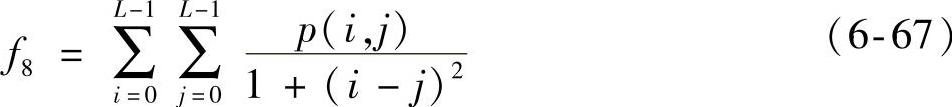
逆差矩又称为局部平稳,它是图像纹理局部变化的度量,反映了纹理的规则程度。纹理越规则,值就越大。反之亦然。
(9)和平均
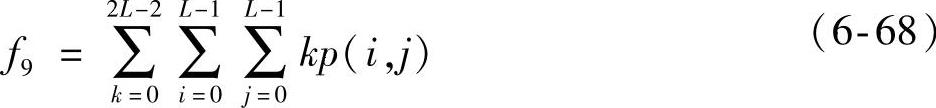
式中,k=i+j。和平均是图像区域内像素点平均灰度值的度量,适用于灰度图像。
(10)差平均

(11)差方差
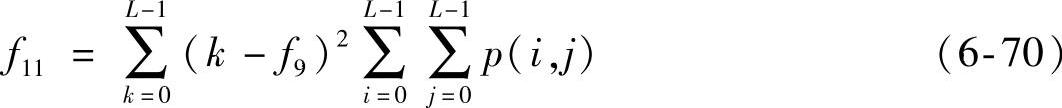
差方差是邻近像素灰度值差异的方差,若像素对比得越强烈,值越大。
(12)差熵
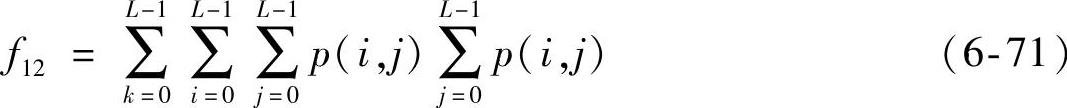
式中,k=i-j。
(13)和熵
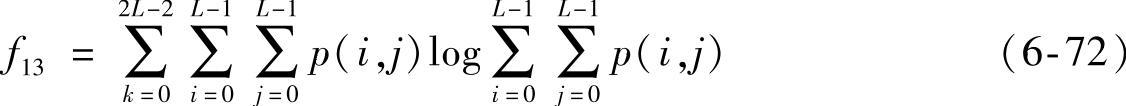
式中,k=i+j。
和熵、差熵代表的意义参考熵。
综上所述,取不同的θ、d和灰度级组合就会生成不同的共生矩阵,得到的特征参数值也就不同,这样描述纹理的能力也会有差异。因此,通过分析特征参数,可以得到纹理的不同描述。
