11.2.1  CCA的数学描述

11.2.1 CCA的数学描述

设有两随机变量组X=[X₁，X₂，…，X_p]′和Y=[Y₁，Y₂，…，Y_q]′，不妨设p≤q。

对于X、Y，设第一组变量的均值和协方差矩阵为E（X）=μ₁，cov（X）=Σ₁₁。

第二组变量的均值和协方差矩阵为E（Y）=μ₂，cov（Y）=Σ₂₂。第一组与第二组变量的协方差矩阵为cov（X，Y）=Σ₁₂=Σ₂′₁。于是，对于矩阵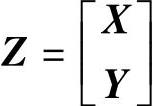有均值向量

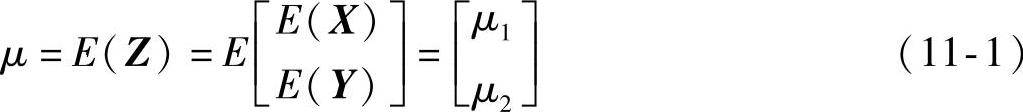
则协方差矩阵为

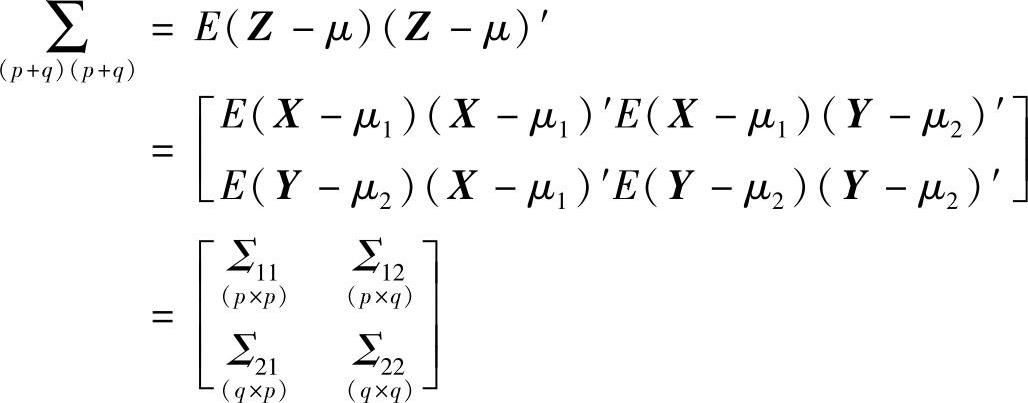
要研究两组变量X₁，X₂，…，X_p和Y₁，Y₂，…，Y_q之间的相关关系，首先分别作两组变量的线性组合，即

U=a₁X₁+a₂X₂+…+a_pX_p=a′X

V=b₁Y₁+b₂Y₂+…+b_qY_q=b′Y（11-2）

式中，a=（a₁，a₂，…，a_p）′，b=（b₁，b₂，…，b_q）′为任意非零常系数向量，则可得

var（U）=a′cov（X）a=a′Σ₁₁a

var（V）=b′cov（Y）b=b′Σ₂₂b

cov（U，V）=a′cov（X，Y）b=a′Σ₁₂b式中，U与V称为典型相关变量，它们之间的相关系数ρ称为典型相关系数，可以由下式求出ρ：

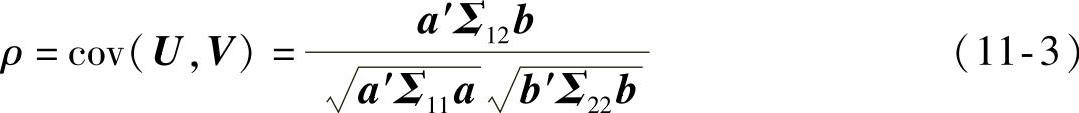
式中，Σ₁₁为变量X的协方差矩阵；Σ₂₂为变量Y的协方差矩阵；Σ₁₂为变量X与Y的互协方差矩阵。