12.1.3  BP神经网络训练学习

在BP层神经元训练的过程中，主要通过对w_ji不停地进行有效的调整，来帮助神经元达到权值训练的目的，最后使得w_ji与u_i无限接近。当调整到一个极限值时，此时BP神经元的输出是1，但是条件是在BP神经网络隐层中的神经元必须处于w_ji=u_i时，神经元的输出1才会有效。当神经网络内部的训练已经全部结束时，输入层有向量信号输入到此神经网络中，此时在BP神经网络中，它里面的所有神经元，不管是输入层、输出层还是隐层都会根据输入向量与其相应的权值向量对比，如果互相比较接近就对其进行有效的结果输出。如果在相应的对比过程中出现与权值向量的差距比较大，这时神经网络的输出是个非常小的数，反之就是上述提到的输出为1。因为BP神经网络中的输出层可以为线性，若此时输出层的神经元是线性函数，则此时的神经网络输出是经过加权并求和作为输出的结果。通过理论分析和推导得出的结论是，在BP内部只要存在所需要的神经元个数，此时BP神经网络能够精确地无限逼近存在的任何有效函数。

BP神经网络中还必须选取合适的参数，其中隐层中神经元的个数确定是主要参数问题，其中主要对神经网络中的层数、神经元总数、设置初始值、学习速率和期望误差等进行分析。在3层BP神经网络中，根据式（12-7）可知，它是可以将n维向m维空间进行映射，这样就能够对任何函数进行逼近。在隐层中的神经元，因为神经元的数量直接影响了训练的效果，进而影响最终的识别结果。但是当在隐层的神经元数量过大的时候，这时候网络是非常复杂的，这样会导致训练时间过长。一般都是通过在一定范围内进行随机取数的方式来解决，当然也可以通过以下公式来作为理论参考，即

式中，r代表隐层中神经元的总数，m代表输入层中神经元的个数，n代表输出层中神经元的个数，j一般在1～10中取整。

除上述以外，我们还得对权值进行相应的初始化，它的大小直接关系到学习的时间长短，一般取值是在（-1，1）或者[-2.4/n，2.4/n]中的随机数，其中n表示输入特征量的数目。为了保证系统能够稳定对输入的样本进行学习和训练，学习率一般在0.01～0.8之间进行取值。最后就是设置期望误差，这是决定神经网络学习迭代的一个重要条件。

图12-3是BP神经网络学训练习训练的具体流程图。

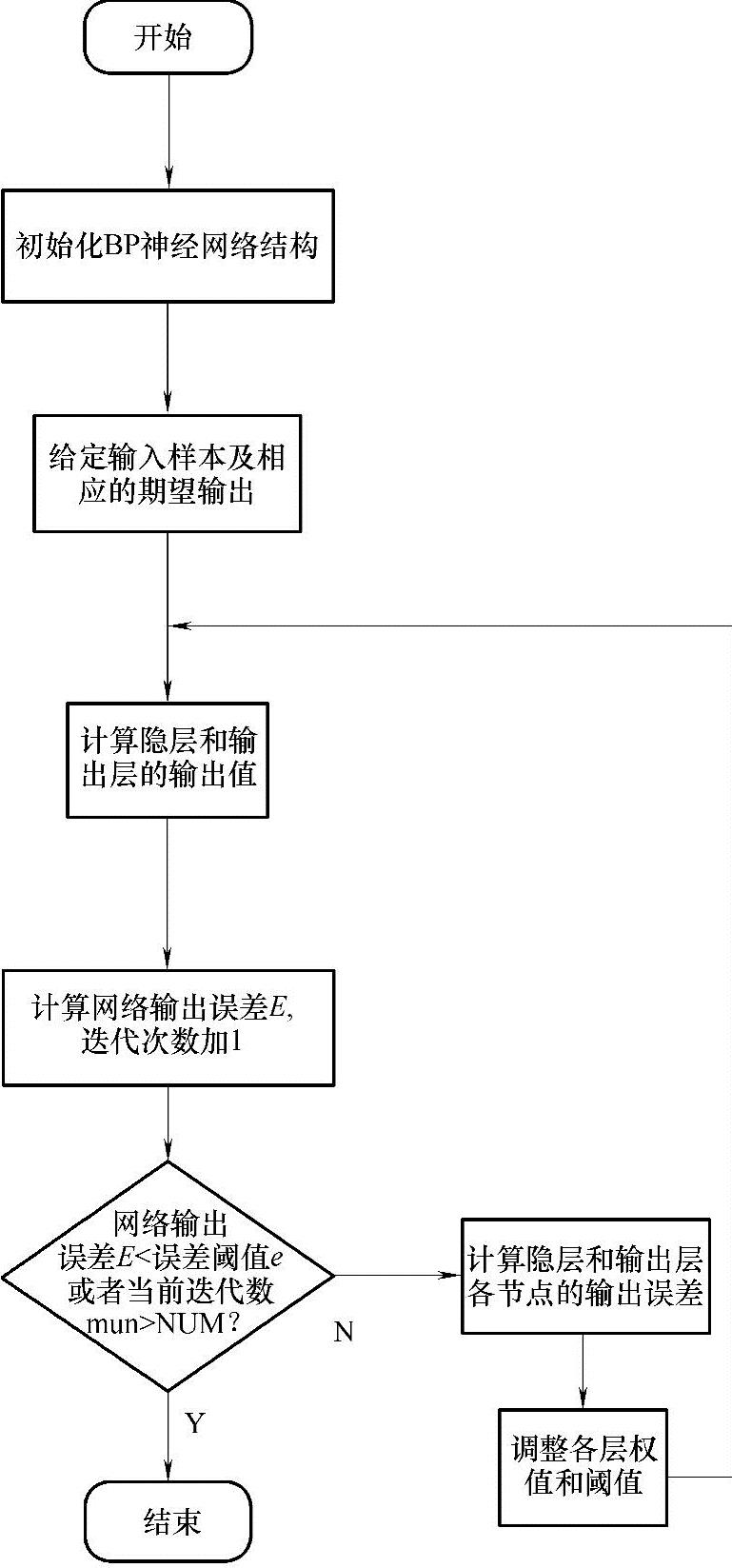
图12-3 BP神经网络训练流程图