6.1.2 多项式不变矩
6.1.2.1 几何矩
在直角坐标系中，连续函数f（x，y）的p+q阶几何矩定义为
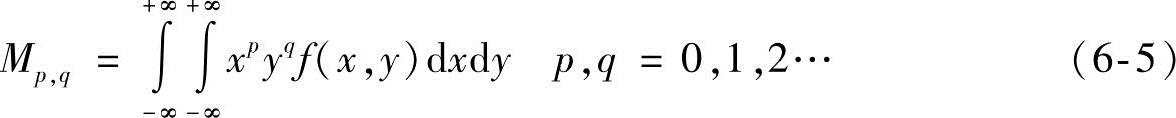
这种矩是将函数f（x，y）投影到xpyq上，其中基本集{xpyq}具有完备性、不正交性。
唯一性定理：如果函数f（x，y）分段连续，且只在（x，y）的有限区域有非零值，则所有阶的矩都存在。由f（x，y）可唯一确定矩序列{Mpq}；反之，由矩序列{Mpq}也可唯一确定f（x，y）。
一幅图的面积必然有限和分段连续，因此，图像的所有阶矩必然存在，用这些矩描述图像具有唯一性。理论上，表征图像的所有信息，需要计算无限多矩值。而实际应用中，只需计算包含足够多图像信息的矩值子集就行。
下面分别介绍各低阶矩及其物理意义：
（1）零阶矩
由式（6-5）的定义可知，图像f（x，y）的零阶矩为
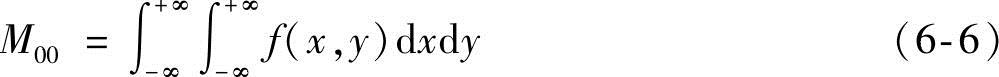
由上式可知，对于一幅灰度图像，M00表示图像所有灰度值的和；对于一幅二值图像，M00表示图像面积。
（2）一阶矩
图像f（x，y）的一阶矩M01和M10可用来表示图像重心。设图像重心坐标为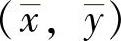
，计算公式为
对于二值图像（x，y）来说它表示几何中心。若把图像重心与坐标系原点重合，令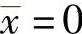
，
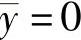，那么式（6-7）就为图像中心矩。这样计算出的矩就与图像坐标系无关。中心矩计算公式为
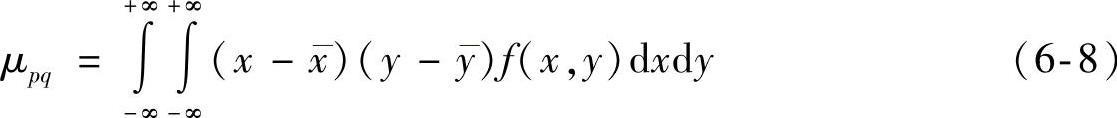
由上式计算可得，一阶中心矩μ01，μ10满足μ01=μ10=0。
（3）二阶矩
二阶中心矩μ02，μ20，μ11，又称惯性矩。可用来描述物体的主轴和椭圆等重要特性。物体目标的主轴由长轴和短轴组成，它们分别表示最大和最小二阶矩的方向。主轴的方向角θ的公式为
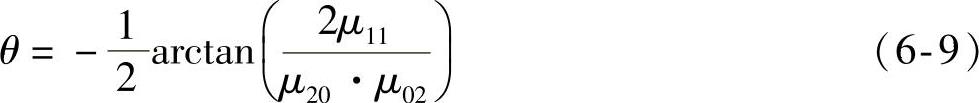
式中，θ为主轴与坐标轴的夹角，它的取值范围为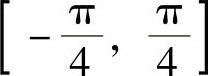
，见表6-1。
表6-1 主轴方向的确定
需要说明的是，仅使用主轴角并不能确定物体目标的方向。比如物体旋转180°后，主轴的方向不变，这就需要利用三阶中心矩，只有这样才能唯一确定物体方向。由一、二阶中心矩还可确定一个图像椭圆。图像椭圆就是一个与原图像的二阶矩和灰度总和都相等的椭圆。椭圆有长半轴a和短半轴b，定义为
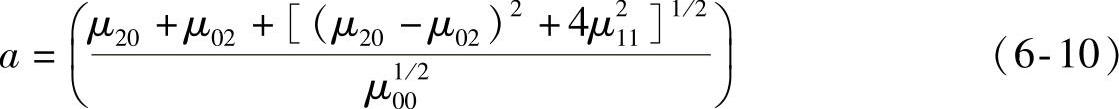
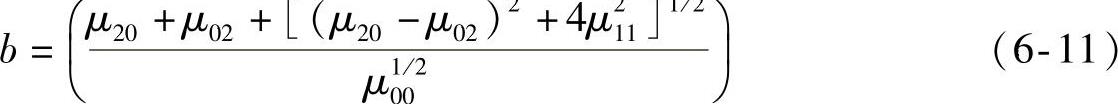
椭圆内的灰度表示为
为了便于分析图像性质，一般将图像重心与椭圆中心和主轴方向重合，如图6-1所示。
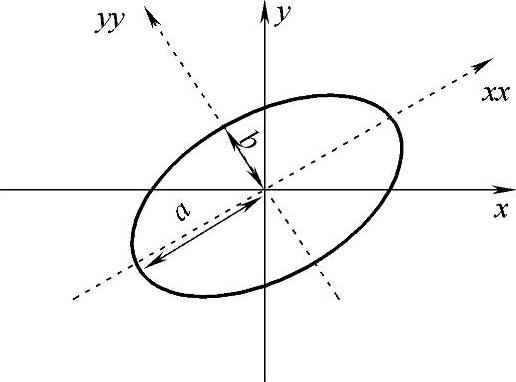
图6-1 图像椭圆
（4）三阶矩
三阶中心矩μ30和μ03描述图像投影后的扭曲程度。扭曲可用来衡量均值对称分布中的偏差程度。式（6-13）、式（6-14）为图像在x，y轴投影的扭曲系数计算公式：
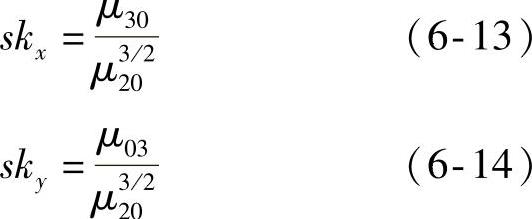
扭曲系数的正负与图像扭曲的关系见表6-2。对于前面提到的主轴方向的问题，是根据扭曲系数的正负来确定的。
表6-2 扭曲系数的正负与图像扭曲的关系
（5）四阶矩
四阶中心矩μ40和μ04又称投影峰度。式（6-15）、式（6-16）为图像在x，y轴投影的投影峰度系数计算公式：
式中，令峰度系数等于0，为高斯分布；小于0，为平坦而少峰的分布；大于0，为狭窄而多峰的分布。
几何矩经过简单变化，就可以满足平移、缩放和旋转不变性。
平移变换：将图像f（x，y）在x轴和y轴方向分别平移a和b，平移后的图像f′（x，y）表示为
f′（x，y）=f（x-a，y-b）（6-17）
图像f′（x，y）的p+q阶矩为
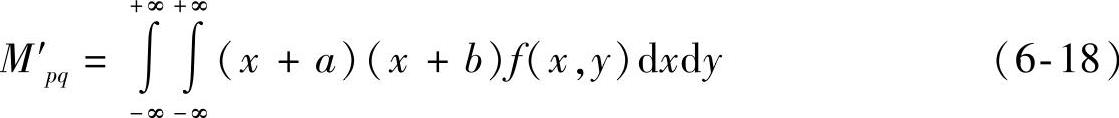
设数字图像为g（m，n），则式（6-18）变换为
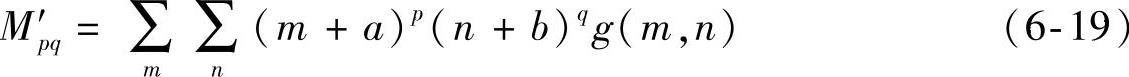
平移前后矩Mpq和M′pq的关系为
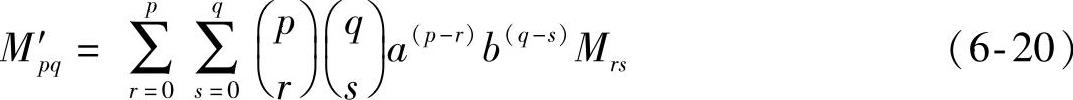
由式（6-20）可得图像f（x，y）的p+q阶中心矩为
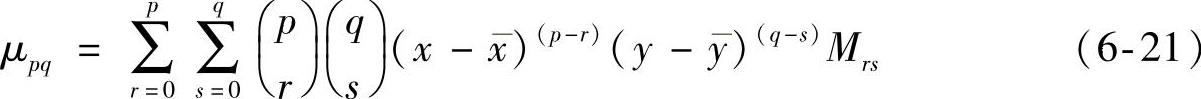
则平移变换前后有
比例变换：将图像f（x，y）在x轴和y轴方向分别缩放α，β倍，则比例变换后的新图像f′（x，y）为
f′（x，y）=f（x/α，y/β）（6-23）
变换前后的矩Mp′q和Mpq关系如式（6-24）、式（6-25）所示：
Mp′q=α1+pβ1+qMpqα≠β（6-24）
Mp′q=α2+p+qMpqα=β（6-25）
令M00=1就可实现图像比例归一化。对于二值图像，可以把图像面积的值设为1。实现归一化的尺度因子表示为
归一化后原点矩为
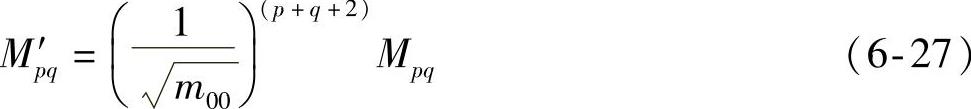
通过上述的处理方法，可得出具有比例（缩放）不变性的中心矩为
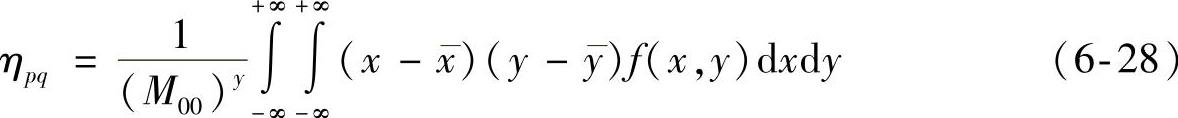
式中，
旋转变换：将图像f（x，y）绕坐标原点作逆时针θ角度旋转后，得到的图像f′（x，y）为
f′（x，y）=f[（xcosθ+ysinθ），（-xsinθ+ycosθ）]（6-30）
旋转变换后图像f′（x，y）的p+q阶矩为
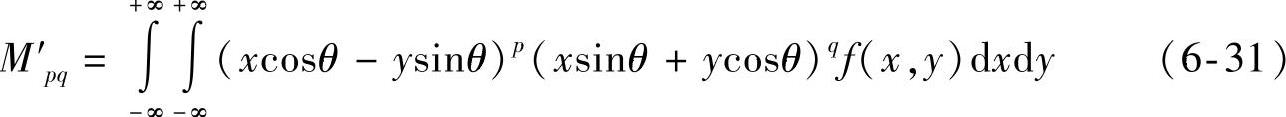
对于数字图像g（m，n），式（6-31）变为
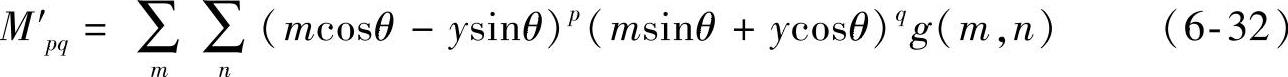
旋转变换前后的矩Mpq和Mp′q的关系如下：
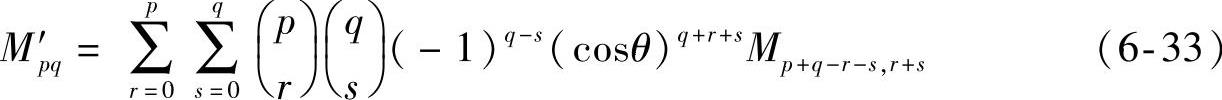
采用主轴法可以实现矩的旋转不变性。对于有唯一分布的主轴图像，计算它的各阶矩，这些矩在分布方向上是不变的。令μ11=0，可得到主轴。
归一化后标准矩定义如下：
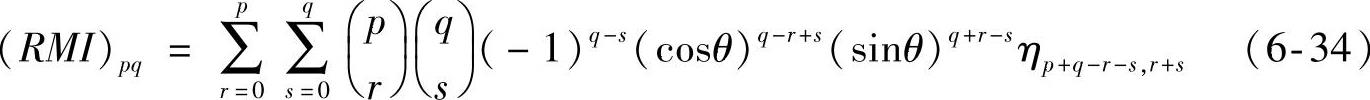
6.1.2.2 Hu矩的构造
事实上，几何矩Mpq并不具有不变性；图像的中心矩μpq仅具有平移的不变性；归一化中心矩有多种构造方式。
方式一为
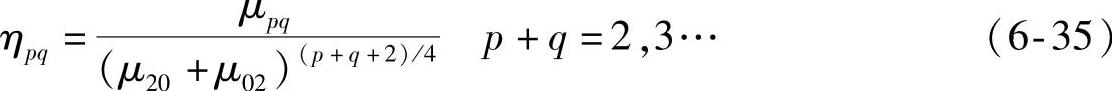
另一种方式为
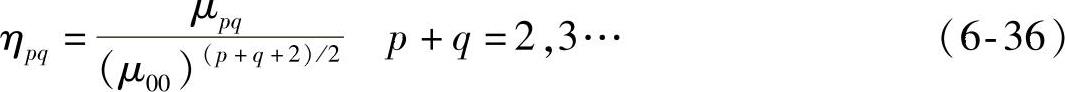
归一化的中心矩ηpq具有平移和比例不变性，但不具有旋转不变性。针对这一问题，Hu在1961年给出了七个不变矩特征量，并证明了它们具有平移、比例不变性和旋转不变性的性质。七个不变矩多项式表达式为
M1=η20+η02（6-37）
M2=（η20-η02）2+4η211（6-38）
M3=（η30-3η12）2+（3η21-η03）2（6-39）
M4=（η30+3η12）2+（η21+η03）2（6-40）
M5=（η30-3η12）（η30+η12）[（η30+η12）2-3（η21+η03）2]+（6-41）
（3η21-η03）（η21+η03）[3（η30+η12）2-（η21+η03）2]
M6=（η20-η02）[（η30+η12）2-（η21+η03）2]+4η11（η21+η03）（η30+η12）
（6-42）
M7=（3η21-η03）（η30+η12）[（η30+η12）2-3（η21+η03）2]+（6-43）
（η30-3η12）（η21+η03）[3（η30+η12）2-（η21+η03）2]
由于七个不变矩值的变化范围很大，为了便于比较，可利用取对数的方法进行数据压缩。因此，实际采用的不变矩为
Mk=logMkk=1，2，…，7（6-44）
Hu不变矩的计算流程如图6-2所示。
图6-2 Hu不变矩的计算流程
表6-3为对坦克图片Hu矩的特征提取结果。
表6-3 坦克Hu矩特征提取结果
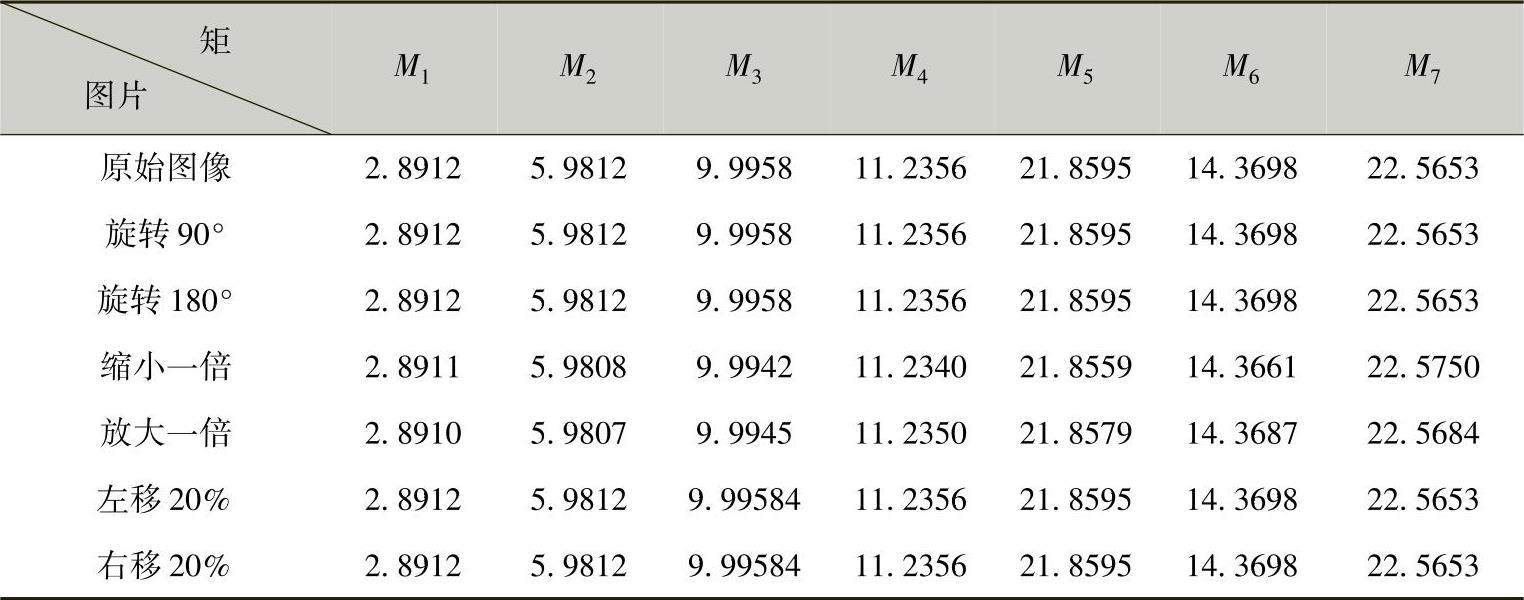
由表6-3中数据可知，通过对坦克图片进行旋转、尺度和平移变换，Hu矩提取的特征参数不发生变化，满足矩不变性。6.1.2.3 仿射不变矩的构造
Hu提出的不变矩具有平移、尺度和旋转不变性，但当由于拍摄角度不同，图像出现扭曲等变形时，这三个不变性并不能满足要求，因此需要构造一种目标发生扭曲、拉伸等仿射变换条件下的不变矩特征。此特征能用于不同拍摄角度下目标的识别。
仿射变换是一种典型的线性变换，它是通过不同的线性变换进行构造的。设图像平面上一点P的坐标为（x，y）和对应仿射变换坐标系中点P′的坐标为（x′，y′），则其二维的仿射变换公式如下：
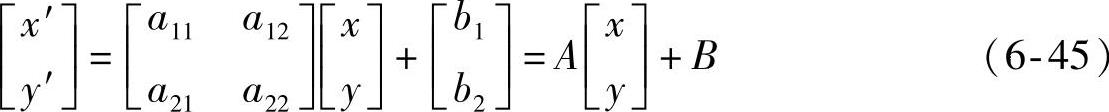
式中，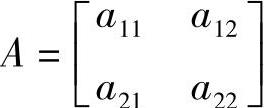
是仿射变换矩阵。仿射变换矩阵A必须满足非奇异性条件，即
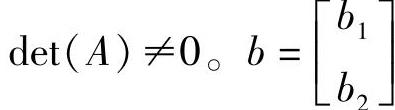是平移量，在二维矩阵空间中，矩阵A可以按扭曲、伸缩、尺度、旋转等进行构造。
尺度变换模型为
伸缩变换模型为
扭曲变换模型为
旋转变换模型为
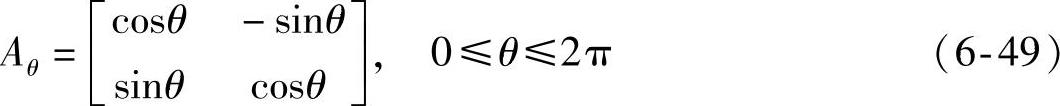
因此，矩阵A可表示为
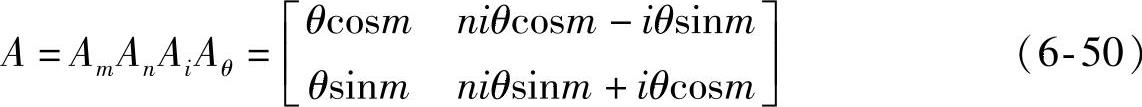
尺度、平移、伸缩、旋转和扭曲五个变换是仿射变换中的特例。
由仿射变换模型可知，如果一个特征量，在尺度、平移、伸缩、旋转和扭曲变换条件下仍然不发生变换，那么我们就认为该特征量是仿射不变量。
设图像f（x，y）仿射变换后的图像为fT（x，y），则仿射变换后图像的重心变为
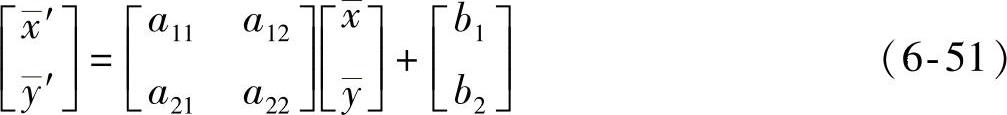
把式（6-45）与式（6-51）相减，得
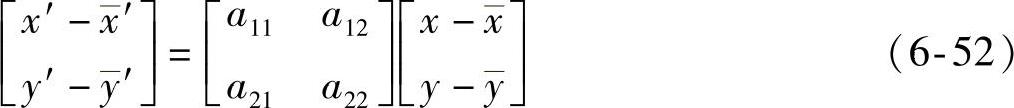
平移参数b1、b2被抵消掉。
由前面的内容可知，归一化中心具有比例、平移和旋转不变性。若利用归一化中心矩来构造仿射不变矩，只需要满足扭曲和拉伸不变性，就可达到仿射变换不变性。我们可以构造中心矩多项式，来抵消仿射变换矩阵A，就可满足常用的仿射不变性。构造多项式的方法有配极多项式、Hankel行列式、多项式判别式等方法。本章采用JanFlusser等人构造的6个仿射不变矩，作为目标图像的特征不变量，进行目标识别。
I1=（μ20μ02-μ211）/μ400（6-53）
I2=（μ230μ203-6μ30μ03μ21μ12+4μ03μ231+4μ30μ312）/μ0100（6-54）
I3=（μ20（μ21μ03-μ212）-μ11（μ30μ03-μ21μ12）+μ02（μ12μ30-μ221））/μ700 （6-55）
I4=（μ230μ203-6μ220μ11μ12μ03-6μ220μ02μ21μ03+9μ220μ03μ212+12μ20μ211μ21μ03+
6μ20μ11μ02μ30μ03-18μ20μ11μ02μ21μ12-8μ311μ03μ30-6μ20μ202μ30μ12+
9μ20μ202μ221+12μ211μ02μ30μ12-6μ11μ022μ30μ21+μ302μ230）/μ0101（6-56）
I5=（μ40μ04-4μ13μ31+3μ222）/μ600（6-57）
I6=（μ04μ22μ40+2μ13μ22μ31-μ04μ231-μ40μ213-μ232）/μ090（6-58）
仿射不变矩的计算流程如图6-3所示。
图6-3 仿射不变矩的计算流程
表6-4为坦克图片仿射不变矩提取结果。
表6-4 坦克图片仿射不变矩的特征提取结果
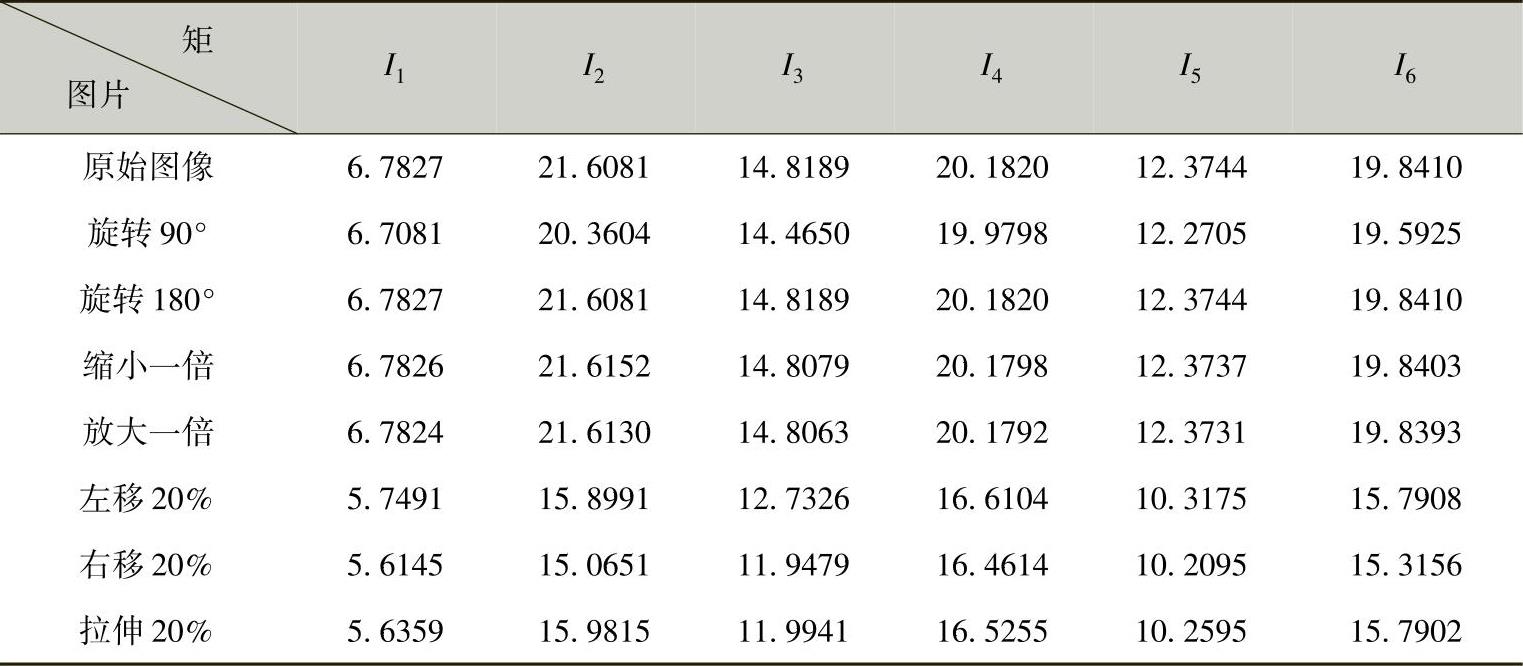
由表6-4中数据可知，当对坦克图片进行旋转、放缩变换时，仿射不变矩不发生变化，对图片进行平移和拉伸变换时，提取的特征参数基本不发生变化，满足矩不变性。