10.2  随机变量的独立性概念

10.2 随机变量的独立性概念

统计独立性是构成ICA基础的一个关键概念。考虑两个不同随机变量x和y的情形，如果知道随机变量y的值并不能给出随机变量x取值的任何信息，那么我们说x独立于y。数学上，统计独立性是通过联合概率密度函数来定义的。若随机变量x和y为独立的，需要满足式（10-4）的条件：

p_x，y（x，y）=p_x（x）p_y（y）（10-4）

换句话说，x和y的联合概率密度p_x，y（x，y）必须能分解成它们的边缘密度p_x（x）与p_y（y）的乘积。可以通过累积分布函数等价地来定义：在式（10-4）中将概率密度函数换成相应的累积分布函数，那么联合累积分布函数也必须是可分解的。

满足独立性的随机变量具有如下基本性质：

E{g（x）h（y）}=E{g（x）}E{h（y）}（10-5）

式中，g（x）和h（y）分别是关于x和y的任意绝对可积函数。这是因为：

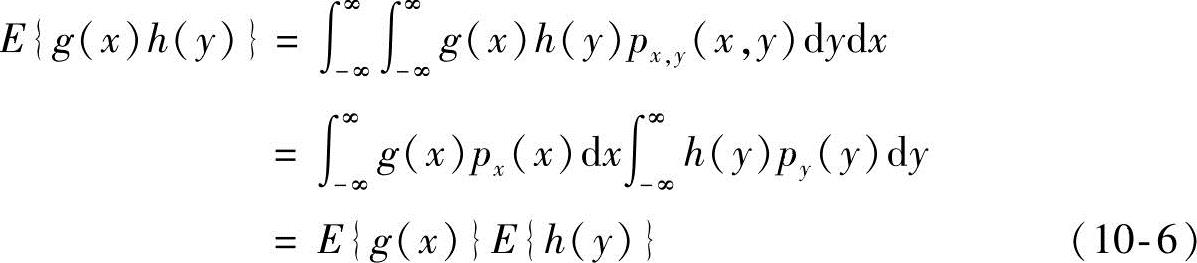
由式（10-4）可以推广到多个随机变量的情形。令x，y，z…是随机向量，

则x，y，z…的独立性条件见式（10-7）：

p_x，y，z…（x，y，z…）=px（x）p_y（y）p_z（z）… （10-7）

而基本性质式（10-5）则推广为式（10-8）所示：

E{g_x（x）g_y（y）g_z（z）…}=E{g_x（x）}E{g_y（y）}E{g_z（z）}… （10-8）

式中，g_x（x）、g_y（y）和g_z（z）分别是随机变量x、y、z的任意函数，要求这些函数使得式（10-8）中定义的期望存在。

式（10-8）给出了统计独立性标准观念的一种推广。随机向量x的分量本身就是标量值的随机变量，y和z也是一样。显而易见，x的各分量之间是可以相互关联的，但需要与其他随机向量的分量之间相互独立，对随机向量y和z也有类似的论断，这样才能使得式（10-8）成立。